---
title: VISI601_CMI TP1 Algèbre linéaire numérique
---
# TP1 - Algèbre linéaire numérique
> [name=Jacques-Olivier Lachaud][time=February 2022][color=#907bf7][time=March 2024]
###### tags: `visi601_cmi` `tp`
Retour à [VISI601_CMI (Main) Algorithmique numérique](https://codimd.math.cnrs.fr/s/IWTaBkA9m)
---
[TOC]
---
## Introduction
Ce TP vous fait travailler les points suivants:
- programmation Python, bibliothèque numpy
- résolution de systèmes linéaires
- décomposition LU, décomposition LU avec choix de pivot
- stabilité numérique des algorithmes
- efficacité des algorithmes (e.g. algorithmes lignes ou colonnes)
- matrices pleines / matrices creuses
La décomposition LU est à la base de la résolution des systèmes linéaires de la forme $A\mathbf{x}=\mathbf{b}$. Ce TP vous fait comprendre en détails les décompositions matricielles. Evidemment, ces algorithmes sont déjà implémentés en Python, mais il s'agit ici de vous les faire comprendre, et notamment d'identifier quelle variante d'algorithme doit être utilisée suivant la représentation choisie des matrices.
Vous trouverez beaucoup de documentation utile sur python et numpy à ces adresses:
- python (v3): https://docs.python.org/3/
- numpy: https://docs.scipy.org/doc/numpy/reference/routines.html
- numpy.linalg: https://docs.scipy.org/doc/numpy/reference/routines.linalg.html
On peut aussi utiliser scipy, qui partage beaucoup de fonctionnalités avec numpy, mais qui en ajoute beaucoup d'autres. En fait, scipy est plus dépendant de bibliothèques optimisées tierces, notamment LAPACK, écrite en FORTRAN. Les matrices creuses font partie de scipy.
**A rendre**: Vous me ferez une archive contenant le ou les programmes python, ainsi qu'un compte-rendu donnant l'état d'avancement et les différentes choses demandées dans l'énoncé. Il sera tenu compte dans la notation du respect des consignes, de la qualité de code, mais aussi de la façon dont chaque partie du travail demandé est testée (dans le compte-rendu ou dans le code lui-même). Vous me remettrez une première version dans une archive (zip ou tar.gz) via <a href="https://tplab.apps.math.cnrs.fr">TPLab</a> à la fin de la séance. Le TP est assez long, donc ne soyez pas surpris si vous n'avez pas terminé à la fin de la matinée. Vous avez jusqu'au mardi 26 mars minuit pour me remettre une version finale, via TPLab aussi. Le TP peut être fait en monôme ou binôme.
> [color=#ff0000] Pensez à simplifier le travail de l'évaluateur. Si vous faites des fonctions et un main python, affichez des traces précisant quelle question est traitée et si elle est fonctionnelle. Une autre possibilité est de faire un notebook jupyter, avec des commentaires à chaque étape. Faites des tests type pour chaque question.
## I Environnement(s) de développement Python
Vous allez écrire du code Python simple. On utilise le module `numpy`
essentiellement pour avoir la structure de données représentant les
matrices pleines, et `scipy` pour les matrices creuses. Le développement peut se faire indifféremment sous Linux, Mac ou Windows, du moment que vous avez Python3, numpy/scipy.
### I.1 Test si vous avez numpy/scipy
Dans votre terminal, tapez
```shell
python -c 'import numpy; print( numpy.__version__)'
python -c 'import scipy; print( scipy.__version__)'
```
Cela devrait vous donner le numéro de version, ou un erreur sinon.
### I.2 Installation si numpy et/ou scipy ne sont pas installés
#### avec python/pip
Sous Linux, si numpy/scipy n'est pas installé, il suffit de taper dans un terminal:
```shell
pip install --user numpy
#python -m pip install numpy
pip install --user scipy
#python -m pip install scipy
```
`IDLE` est un exemple de petit environnement de développement intégré Python (https://docs.python.org/3/library/idle.html).
#### avec conda
Anaconda est un système de gestion de packages python. En général, on crée un environnement, puis on installe les bibliothèques voulues.
```shell
# Best practice, use an environment rather than install in the base env
conda create -n info601
conda activate info601
# If you want to install from conda-forge
conda config --env --add channels conda-forge
# The actual install command
conda install numpy scipy
```
#### notebook jupyter
Une autre solution est d'utiliser un notebook `Jupyter`. Vous tapez et
exécutez les commandes dans un navigateur web. Vous avez des serveurs
en ligne: https://jupyter.org/try
Pour utiliser simplement `numpy`, vous pouvez mettre les lignes suivantes au début de votre module.
```python=
import numpy as np
import numpy.matlib as mat
import numpy.linalg as lin
```
### I.3 Vérifiez votre environnement
Si votre environnement fonctionne, le bout de code suivant (avec les lignes au-dessus) doit fonctionner:
```python=
A = np.array( [ [1., 3., -2.], [4., -1., 5.], [2., 5., 10.] ] )
# determinant
print( "det(A)=", lin.det(A) )
# conditionnement
print( "cond(A)=", lin.cond(A) )
# inverse
print( "A^-1=", lin.inv(A) )
```
Si vous avez installé `scipy`, vous pouvez déjà voir la décomposition LU de A avec pivot partiel.
```python=
import scipy
import scipy.linalg
P,L,U=scipy.linalg.lu(A)
tP = P.transpose()
print( "tP=", tP )
print( "L=", L )
print( "U=", U )
print( "tPA=", np.matmul(tP,A) )
print( "LU=", np.matmul(L,U) )
```
### I.4 Avertissement sur le calcul scientifique avec python/numpy
> **Important** Python a tendance à faire beaucoup de choses implicitement, car il ne gère pas le typage comme des langages comme le C++ ou le JAVA. Des erreurs de transtypage bizarres sont fréquents. L'exemple ci-dessous est frappant:[color=#d00000]
```python=
# avec des entiers 0.5
a = 1 # a est un entier
a /= 2 # change le type de a en double
print( a ) # affiche (assez) naturellement 0.5
```
```shell
0.5
```
```python=
# avec des matrices
A = np.asmatrix( np.array([[1,0],[0,1]])) # A est une matrice d'entiers
A[0,0] /= 2 # le type de chaque élément de A n'est pas changé
print(A) # affiche la matrice avec le premier coefficient nul !
```
```shell
[[0 0]
[0 1]]
```
> **Important** Une autre erreur courante en python est de croire qu'une affectation `a=b` crée un clone de `b` avec la même valeur. Ce n'est vrai que pour les types simples (genre entiers, réels). C'est faux pour les objets, dont les matrices. [color=#d00000]
```python=
A = np.asmatrix( np.array([[1,2],[3,4]])) # A est une matrice d'entiers
B = A # B désigne en fait la même matrice que A
B[0,0] = 5 # B et A sont changés !
```
:::warning
- Quand vous créez une matrice/np.array, choisissez le type approprié pour les coefficients: `np.array((m,n),dtype=np.double)`
- Quand vous voulez faire une nouvelle matrice égale à A, écrivez `B=A.copy()`
:::
## II Matrices, matrices triangulaires L, U, résolution Ly=b, Ux=y
### II.1 Matrices
On utilisera de manière sous-jacente les classes définies dans `numpy`:
- `array` : une représentation des tableaux à d-dimensions, la classe/structure de données qu'on utilisera partout pour représenter des matrices pleines ou des vecteurs.
- `asmatrix` : donne une vue sur un `array` comme une matrice, et fournit des opérations supplémentaires (multiplication, puissance, max, etc), mais ne semble plus recommandé pour les dernières versions.
```python=
# une matrice 2x3
M = np.asmatrix( np.array([[1,2,3],[4,5,6]]))
# identite I de taille n x n
I = np.asmatrix( np.eye( n ) )
# zeros Z de taille n x n
Z = np.asmatrix( np.zeros( (n,n) ) )
```
On accède à la ligne i (entre 0 et n-1) et à la colonne j (entre 0 et m-1) d'une matrice A avec `A[i,j]` en lecture comme en écriture.
Créer une fonction `hilbert( n )` qui construit et retourne la matrice
de Hilbert dont les coefficients sont de la forme $1/(i+j+1)$ (avec i et
j qui démarre à 0).
```python=
def hilbert( n ):
...
```
Vérifiez que le conditionnement de la matrice augmente très vite avec n, avec `lin.cond(...)`.
### II.2 Résolution de systèmes à matrices triangulaires
Ecrivez les fonctions `solveL` et `solveU` qui résolvent des systèmes
triangulaires inférieurs et supérieurs respectivement.
```python=
def solveL( L, b ):
...
def solveU( U, c ):
...
```
On rappelle la formule de descente (la formule de remontée est similaire)
$$
x_1 = \frac{b_{1}}{l_{11}}, \quad \forall i =2, \ldots, n,
x_i = \frac{1}{l_{ii}} \left( b_{i} - \sum_{j=1}^{i-1} l_{ij}x_j \right).
$$
> **Attention** les indices commencent à 0 en python, à 1 dans les formules mathématiques comme ci-dessus.[color=#d00000]
> On utilisera opportunément la fonction `order` qui vous retourne
l'ordre d'une matrice carrée. Le code ci-dessous vous montre aussi comment on commente les fonctions en python, ce qui peut vous inspirer !
```python=
def order( A ):
"""
Retourne l'ordre d'une matrice carrée A
:param A: une matrice n x n
:return: son ordre n
"""
assert A.shape[ 0 ] == A.shape[ 1 ], "[order] matrix A is not square"
return A.shape[ 0 ]
```
Les fonctions `solveL` et `solveU` sont des méthodes orientées
"lignes", car leurs boucles internes sont sur les lignes. On verra que
ce ne sera pas toujours efficace lorsque les matrices seront creuses.
Validez vos fonctions. Par exemple pour `solveL`, exécutez les lignes suivantes:
```python
L=np.asmatrix( [[ 1.,0., 0., 0.],[0.33333333,1.,0.,0.],[0.5,1.,1.,0.],[0.25,0.9,-0.6,1.]] )
b=np.asmatrix( [[1.],[3.],[2.],[4.]])
y=solveL(L,b)
print("y=",y)
print("L*y=", L*y)
print("b=", b)
print(lin.norm(L*y-b,2))
```
> Vérifiez que la norme $\|L\mathbf{y}-\mathbf{b}\|$ est nulle et que le vecteur $\mathbf{b}$ n'a pas été changé par votre fonction ! Python a tendance à **ne pas** créer de nouvelles variables, mais seulement à **référencer** des variables existantes.
## III Décomposition LU
On va maintenant décomposer une matrice A carrée quelconque en le
produit de deux matrices L et U, L triangulaire inférieure, U
triangulaire supérieure.
### III.1 Elimination de Gauss avec pivot sur la diagonale
On rappelle que le principe de l'algorithme est de rendre A
progressivement triangulaire supérieure en soustrayant la première
ligne fois un certain facteur (appelé *multiplicateur*) à toutes les
autres dessous. La première colonne étant vidée, on procède
de même sur les lignes suivantes. Au bout du processus, la
matrice A est la matrice triangulaire supérieure U. La matrice
triangulaire inférieure L est tout simplement la matrices des
multiplicateurs utilisés, plus une diagonale de 1.
$$
\begin{bmatrix}
a^{(1)}_{11} & a^{(1)}_{12} & \ldots & a^{(1)}_{1n} \\
a^{(1)}_{21} & a^{(1)}_{22} & \ldots & a^{(1)}_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a^{(1)}_{n1} & a^{(1)}_{n2} & \ldots & a^{(1)}_{nn} \\
\end{bmatrix}
\quad \Rightarrow
\quad
\begin{bmatrix}
a^{(1)}_{11} & a^{(1)}_{12} & \ldots & a^{(1)}_{1n} \\
0 & a^{(2)}_{22} & \ldots & a^{(2)}_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
0 & a^{(2)}_{n2} & \ldots & a^{(2)}_{nn} \\
\end{bmatrix}
$$
avec
$$
a^{(2)}_{ij} = a^{(1)}_{ij} - m_{i1} a^{(1)}_{1j}, ~\text{pour}~ i,j = 2, \ldots, n
$$
où les multiplicateurs vérifient $m_{i1}=\frac{a^{(1)}_{i1}}{a^{(1)}_{11}}$, pour $i=2,\ldots,n$, et $m_{ii}=1$, et $m_{ij}=0$ pour $j>i$.
Ecrire une fonction `LU(A)` qui retourne les matrices L et U
produites. Comme la décomposition LU peut échouer si un des éléments
diagonaux est nul au cours du processus d'élimination, tester si le
pivot est non-nul et retourner aussi en sortie le rang de sortie (ou
l'ordre de A si tout s'est bien passé).
```python=
def LU( A ):
"""Calcule la décomposition LU et la retourne (L,U)
:param A: une matrice carrée d'ordre n
:return: L,U,k où L et U sont les matrices triangulaires de la
décomposition LU et k est le rang où le processus s'est arrété (n
si tout s'est bien passé).
"""
...
```
Vous pouvez vérifier que votre code fonctionne en le testant sur les matrices (dites de Vandermonde):
```python=
def VDM(x):
n = len(x)
V = np.asmatrix( np.ones((n,n)) )
for i in range(0,n):
for j in range(1,n):
V[i,j] = V[i,j-1]*x[i]
return V
V=VDM([1.5, 2.8, 4.0, 7.3])
L,U,k=LU(V)
```
doit afficher
```shell
(matrix([[1. , 0. , 0. , 0. ],
[1. , 1. , 0. , 0. ],
[1. , 1.92307692, 1. , 0. ],
[1. , 4.46153846, 8.7 , 1. ]]),
matrix([[ 1. , 1.5 , 2.25 , 3.375],
[ 0. , 1.3 , 5.59 , 18.577],
[ 0. , 0. , 3. , 24.9 ],
[ 0. , 0. , 0. , 86.13 ]]),
4)
```
### III.2 Résolution Ax=b par LU
Il ne vous reste plus qu'à résoudre le système $A \mathbf{x}=\mathbf{b}$ en résolvant les deux systèmes suivants: d'abord $L\mathbf{y}=\mathbf{b}$ puis $U \mathbf{x}=\mathbf{y}$, ce qui donnera la solution du système. Ecrire cette fonction `solveByLU`.
```python=
def solveByLU( A, b ):
...
```
### III.3 Application à l'interpolation polynomiale
On a $n+1$ points représentés par les vecteurs $X=(x_0,x_1,\ldots,x_n)$ et $Y=(y_0,y_1,\ldots,y_n)$. On cherche une courbe polynomiale $P(x)$ de degré $n$ qui passe par tous ces points, avec $P(x)=c_0 + c_1 x + c_2 x^2 + \cdots + c_n x^n$
Il est connu qu'il faut résoudre le système linéaire suivant:
$$
\underbrace{
\begin{bmatrix}
1 & x_0 & x_0^2 & \ldots & x_0^n \\
1 & x_1 & x_1^2 & \ldots & x_1^n \\
\vdots & \vdots & \vdots & \vdots & \vdots \\
1 & x_n & x_n^2 & \ldots & x_n^n \\
\end{bmatrix}}_{\mathbf{A}}
\underbrace{
\begin{bmatrix}
c_0 \\ c_1 \\ \vdots\\ c_n
\end{bmatrix}}_{\mathbf{x}}
=\underbrace{
\begin{bmatrix}
y_0 \\ y_1 \\ \vdots\\ y_n
\end{bmatrix}}_{\mathbf{b}}
$$
On vous donne la fonction pour calculer la matrice de Vandermonde d'un
tableau de valeurs:
```python=
def VDM(x):
"""Calcule la matrice de Vandermonde du vecteur x
:param x: un vecteur de doubles [x_0, ..., x_n-1]
:return: la matrice de Vandermonde associée
"""
n = len(x)
V = np.asmatrix( np.ones((n,n)) )
for i in range(0,n):
for j in range(1,n):
V[i,j] = V[i,j-1]*x[i]
return V
```
Vous pouvez vérifier que votre fonction `solveByLU` sur le petit problème suivant:
```python=
X = [1.5, 2.8, 4.0, 7.3]
Y = [3.2, 1.4, 1.0, 2.7]
V = VDM(X)
b = np.asmatrix(Y).transpose()
C = solveByLU(V,b)
print(C)
```
donne
```shell
matrix([[ 7.71496289],
[-4.04867526],
[ 0.75245648],
[-0.03999321]])
```
Le bout de code suivant permet de tracer les points formés par X,Y en rouge et le polynome d'interpolation en bleu.
```python=
import matplotlib.pyplot as plt
ax=plt.subplot()
xvals = np.arange(0, 10, 0.01)
yvals = [C[0].item()+C[1].item()*x+C[2].item()*x*x+C[3].item()*x*x*x for x in xvals]
ax.plot(xvals, yvals)
ax.plot(X,Y,color="red")
plt.show() # necessary if you are not in a jupyter notebook
```
| 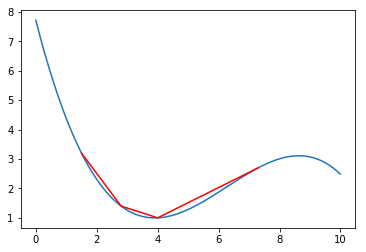 |
| -------- |
| Interpolation de Lagrange de 4 points |
Ecrivez une fonction `tracePolynomeLagrange(X,Y)` qui prend deux tableaux X
et Y et trace la courbe associée. On prendra comme intervalle de tracé
$x_0$ à $x_n$.
> Pour plus d'information sur les tracés de courbe, cette petite introduction devrait faire l'affaire: http://courses.csail.mit.edu/6.867/wiki/images/3/3f/Plot-python.pdf
On peut observer le fameux phénomène de Runge sur le petit exemple suivant, ce qui explique qu'on utilise peu ce type d'interpolant en pratique:
```python=
X = [0. , 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9.]
Y = [0.1, 0.0, 0.05,0.1, 0.0,0.1,0.02,0.07,0.0,0.05 ]
tracePolynomeLagrange(X,Y)
```

> *(pour information)* On peut trouver les solutions d'un système basé sur une matrice de Vandermonde de façon analytique.
### III.4 Stabilité numérique de LU
On va observer la précision numérique de LU sur les matrices de Hilbert. Comment évolue le résidu $\| A\mathbf{x} - \mathbf{b} \|$ en fonction de $n$ ?
```python=
H=hilbert(10)
L,U,k=LU(H)
b=np.asmatrix( np.ones( (order(H),1) ) )
x=solveByLU(H,b)
print(lin.det(H))
print(lin.cond(H))
print(lin.norm(H*x-b))
```
Vérifiez que LU est quand même assez stable, malgré un déterminant nul dès $n=30$ et des conditionnements de la matrice H très grand.
### III.5 Calcul de la matrice inverse
Il est facile de calculer la matrice inverse X de A à partir de LU. Si on note $x_i$ les vecteurs colonnes de X et $e_i$ les vecteurs colonnes de la matrice identité, on voit $A \mathbf{x_i} = \mathbf{e_i}$. Il faut donc résoudre les 2n systèmes linéaires $L \mathbf{y_i} = \mathbf{e_i}$ et $U \mathbf{x_i} = \mathbf{y_i}$ pour toutes les colonnes.
Ecrivez la fonction `inverseByLU( A )` qui calcule cette matrice.
Observez maintenant la stabilité numérique du calcul de la solution à $A \mathbf{x}=\mathbf{b}$ en calculant simplement $A^{-1} \mathbf{b}$.
```python=
n=20
H=hilbert(n)
invA=inverseByLU(H)
b=np.asmatrix( np.ones( (order(H),1) ) )
for i in range(1,n):
b[i] = b[i-1]/2
print(lin.det(H))
print(lin.cond(H))
x = invA*b
print(lin.norm(H*x-b))
```
Est-ce que cette méthode donne un meilleur résultat que LU ? Faites des tests quui montrent que résoudre $LU\mathbf{x}=\mathbf{b}$ est plus précis que calculer l'inverse $A^{-1}$ puis calculer $\mathbf{x}=A^{-1}\mathbf{b}$.
> On ne calcule donc en pratique quasiment jamais l'inverse d'une matrice. Quand bien même elle serait exacte, les erreurs des simples multiplications matrice / matrice sont liées au conditionnement.
### III.6 Elimination de Gauss avec choix de pivot partiel
Attention, même si LU est stable, il peut échouer lamentablement sur des exemples très petits de matrice bien conditionnée, inversible et tout ce qui faut. Cela vient de la représentation des nombres en virgule flottante et de la combinaison de nombres d'ordre de grandeur très différent. Sur le petit exemple de matrice 2x2 ci-dessous, la factorisation LU fait une erreur de 1 en norme !
```python=
H=np.asmatrix( np.array( [[1e-20,1.],[1.,1.]]))
b=np.asmatrix( np.ones( (order(H),1) ) )
L,U,k=LU(H)
# LU - H est très différent de 0
print(L*U-H)
# la solution reste correcte
print(x)
x=solveByLU(H,b)
```
On voit que le problème disparait pour un coefficient 1e-18.
C'est pourquoi on va éviter de prendre des petits pivots dans le calcul de LU. L'idée est de ne pas choisir directement A[k,k] comme pivot, mais de choisir parmi tous les éléments entre A[k,k] et A[n,k] (même colonne).
A chaque pas k de l'algorithme LU, on va donc regarder tous les éléments A[k:n,k] et déterminer le rang r où il y a le plus grand en module/valeur absolue. On va échanger ensuite les lignes k et r de la matrice A. On procède ensuite comme dans LU. Bien sûr, en échangeant les lignes à certains moments, on change le système. Il faut donc mémoriser les permutations successives.
On stockera en plus la permutation courante dans une matrice P. La permutation de deux lignes est simplement une matrice diagonale unité où on a échangé la ligne k avec la ligne r. Les matrices de permutations se composent très facilement (on échangera deux lignes sur la matrice de permutation de l'itération précédente).
Algorithmiquement, on met à jour à chaque itération k la matrice des permutations P en échangeant les lignes k et r (évidemment si $k\neq r$). De plus on échange les lignes k et r de U (entre les colonnes k et n exclu) et de L (entre les colonnes 0 et k exclu). Le reste est inchangé.
Ecrivez la fonction `LUP(A)` qui retourne L,U,P,k. Vérifiez qu'elle
fonctionne sur la matrice Vandermonde suivante:
```python=
X = [1.5, 2.8, 4.0, 7.3]
Y = [3.2, 1.4, 1.0, 2.7]
V = VDM(X)
L,U,P,k = LUP(V)
print(L)
print(U)
print(P)
print(L*U)
print(P*V)
```
```shell
# L
matrix([[1. , 0. , 0. , 0. ],
[1. , 1. , 0. , 0. ],
[1. , 0.43103448, 1. , 0. ],
[1. , 0.22413793, 0.70909091, 1. ]])
# U
matrix([[ 1. , 1.5 , 2.25 , 3.375],
[ 0. , 5.8 , 51.04 , 385.642],
[ 0. , 0. , -8.25 , -105.6 ],
[ 0. , 0. , 0. , 7.02 ]])
# P
matrix([[1., 0., 0., 0.],
[0., 0., 0., 1.],
[0., 0., 1., 0.],
[0., 1., 0., 0.]])
# L*U
matrix([[ 1. , 1.5 , 2.25 , 3.375],
[ 1. , 7.3 , 53.29 , 389.017],
[ 1. , 4. , 16. , 64. ],
[ 1. , 2.8 , 7.84 , 21.952]])
# P*V
matrix([[ 1. , 1.5 , 2.25 , 3.375],
[ 1. , 7.3 , 53.29 , 389.017],
[ 1. , 4. , 16. , 64. ],
[ 1. , 2.8 , 7.84 , 21.952]])
```
### III.7 Résolution Ax=b par LU=PA et stabilité numérique
De même que pour LU, écrivez la fonction `solveByLUP(A,b)` et analyser sa stabilité numérique. Est-elle toujours sensible à la petite matrice 2x2 précédente.
Faites un graphe où vous comparez la stabilité de la résolution de LU=A et de LU=PA (par solveByLU et solveByLUP) sur la matrice de Hilbert en fonction de n.
### III.8 Mesure et amélioration du temps d'exécution de LU et LUP
Vous pouvez mesurer le temps d'exécution avec les commandes `time.time()` (n'oubliez pas le `import time`):
```shell
B=hilbert(100)
start=time.time()
L,U,P=LUP(B)
end=time.time()
print(end-start)
```
Par exemple, vos fonctions LU et LUP prennent à peu près les temps suivants:
```shell
n time( LUP(hilbert(n)) ) en s
10 0.0013
20 0.012
40 0.071
80 0.52
160 3.77
320 29.18
```
> Bien sûr, Python n'est pas très efficace. Si vous utilisez du C ou du Fortran, la décomposition LU prend environ 50 fois moins de temps. Néanmoins, le temps est toujours proportionnel au cube du côté de la matrice. [color=#907bf7]
Vous pouvez néanmoins considérablement améliorer les temps d'exécution avec `numpy` grâce à son système d'accès à des blocs de valeurs via les notations `:` dans ses indices. Par exemple, on peut faire les opérations suivantes
```
# soustrait toute la ligne i à toute la ligne j
A[j,:] -= A[i,:]
A[j] -= A[i] # équivalent
A[j,0:n/2] -= A[i,0:n/2] # seulement la 1ère moitié
# soustrait toute la colonne i à toute la colonne j
A[:,j] -= A[:,i]
```
Utilisez ces opérateurs dans vos fonctions LU et LUP. Vous devriez observer que vos fonctions vont beaucoup plus vite maintenant.
```shell
n time( LUP(hilbert(n)) ) en s
10 0.0017
20 0.0060
40 0.0227
80 0.0917
160 0.3551
320 1.3610
```
> Cela va beaucoup plus vite car `numpy` appelle des fonctions C derrière, qui peuvent alors faire les boucles beaucoup plus rapidement. [color=#907bf7]
## IV Matrices creuses pour les grands systèmes linéaires
Pour certains problèmes, le nombre d'inconnues et le nombre d'équations d'un système linéaire devient vite très important. Pour traiter des images 1000x1000, les matrices utilisées sont de taille 1e6 x 1e6. De même lorsque l'on fait des traitements géométriques de surfaces triangulées. En calcul scientifique, on manipule couramment des matrices encore plus grandes (plusieurs millions de lignes pour de la simulation de fractures mécaniques). On ne peut pas représenter de telles matrices en mémoire et le coût de calcul serait trop élevé.
Or si le nombre d'inconnues et le nombre d'équations d'un système linéaire devient vite très important, dans la plupart des cas chaque équation ne concerne qu'un faible nombre d'inconnues. Les matrices ont donc peu d'éléments différents de zéro par ligne (et souvent aussi par colonne). Quand le nombre d'éléments différents de zéro (noté $n_{nz}$) d'une matrice est petit devant le nombre d'éléments total de la matrice ($n \times n$), on dit que la matrice est **creuse**.
Par exemple, la résolution numérique des EDP obtenue par linéarisation et discrétisation des opérateurs différentiels induit des matrices (très) creuses. Le laplacien sur une grille 2D induit 5 coefficients différents de zéro par ligne.
Le théorème de Gilbert/Preierls montre même que la décomposition LU peut se faire en temps $O(n_{nz})$.
### IV.1 Représentations creuses de matrices
Il y a plusieurs façons de représenter des matrices creuses, chacune ayant ses avantages et inconvénients.
- COO: format triplet ou coordonnées. On stocke des triplets valeur, colonne, ligne.
Pratique pour construire une matrice creuse. Sinon, inefficace.
- CSR: format ligne compressée. Il utilise trois tableaux: le tableau `data` des valeurs de taille nnz, le tableau `indices` de taille nnz qui contient la colonne de chaque valeur, le tableau `indptr` de taille nombre de lignes+1, qui stocke le numéro du premier élément dans sa ligne.
- opérations arithmétiques efficaces CSR + CSR, CSR * CSR, etc.
- extraction d'une ligne rapide
- produit matrices / vecteurs rapides
- mais assez lent d'extraire une colonne ou de faire des mises à jour
- CSC: format colonne compressée. Même principe que CSR, mais par colonne.
- opérations arithmétiques efficaces CSR + CSR, CSR * CSR, etc.
- extraction d'une colonne rapide
- produit matrices / vecteurs rapides (CSR plus rapide)
- mais assez lent d'extraire une ligne ou de faire des mises à jour
Par exemple, l'algorithme SuperLU utilise les formats suivants pour ses calculs: A CSC, L CSR, U CSC.
On vous donne le générateur de matrice laplacienne suivant:
```python=
def gridCooMatrix( n, random=True ):
"""Returns a Laplacian-like matrix for a grid n x n.
Matrix has thus order n*n.
If random=True, indices of vertices are randomly chosen.
"""
V = [] # values
R = [] # rows
C = [] # columns
N=n*n
A = [i for i in range(N)]
if (random):
A = np.random.permutation( N )
for r in range(n*n):
V.append(-4.)
R.append(A[r])
C.append(A[r])
V.append(1.)
R.append(A[(r+1)%N]) # right neighbor
C.append(A[r])
V.append(1.)
R.append(A[(r+N-1)%N]) # left neighbor
C.append(A[r])
V.append(1.)
R.append(A[(r+n)%N]) # down neighbor
C.append(A[r])
V.append(1.)
R.append(A[(r+N-n)%N]) # up neighbor
C.append(A[r])
return sp.coo_matrix( (V,(R,C)), shape=(N,N))
```
On appelle structure d'une matrice A la matrice B de même taille composée de 0 là où A vaut 0, et 1 sinon. Ecrire la fonction `structure(M)` qui retourne la structure de la matrice M (sous forme de matrice **dense** afin de pouvoir l'afficher). Les lignes suivantes devraient vous donner:
```python=
import matplotlib.pyplot as plt
import scipy.sparse as sp
def occupancy(M):
plt.imshow( structure(M) )
M_coo = gridCooMatrix( 10 )
M = M_coo.tocsc()
occupancy( M )
```
| 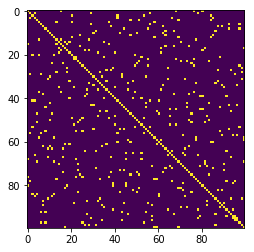 |
| -------- |
| Structure pour le laplacien sur une image 10x10, numérotation aléatoire |
Calculez la structure de la matrice $M^2$. Qu'observez-vous ? Que se passerait-il si on calcule la structure du produit $M^3$, etc ?
> $M^2$ est la matrice approchant le bilaplacien.
### IV.2 Décomposition LU de matrice creuse
On va utiliser le module `scipy.sparse.linalg` pour décomposer M en
LUP (c'est trop compliqué à écrire pour vous encore). La bibliothèque utilisée derrière est SuperLU.
```python=
import scipy.sparse as sp
import scipy.sparse.linalg as spl
# Fabrique un objet SLU
SLU=spl.splu(M,permc_spec="NATURAL")
occupancy(SLU.L)
```
Faites un tableau où vous affichez les taux d'occupations des matrices
et leur structure (vous poursuivrez ce tableau dans les sections
suivantes).
| LU Méthode | M occupancy | L occupancy | U occupancy | $M^{-1}$ occupancy |
| ---------- | -------------- | ----------- | ----------- | ------------------ |
| "NATURAL" | 5% (M 100x100) | 17.6% | 17.6% | 100% |
| |  | 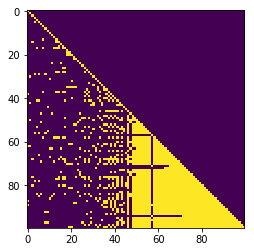 |  | |
On voit que, même si M est creux, L et U sont beaucoup moins creux, et $M^{-1}$ pas du tout.
On peut néanmoins avoir une influence sur le remplissage en faisant des bonnes permutations de lignes et colonnes.
Changez le mode `permc_spec` de `spl.splu` à "COLAMD". Qu'observez-vous ? Les matrices L et U ont-elle changée ? Leur taux d'occupation est-il meilleur ? Complétez votre tableau avec ces informations.
Si on augmente la taille de la matrice M, quel est l'évolution de vos taux d'occupation ?
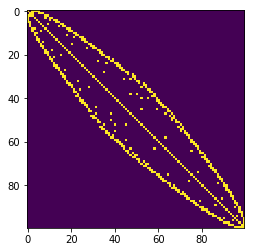
### IV.3 Optimisation de la largeur de bande de la matrice
Le remplissage plus important de L et U vient de la largeur de bande non bornée de M. On peut optimiser cette largeur de bande avec des algorithmes de type parcours dans un graphe. Le plus connu est Reverse Cuthill-McKee. Il fait des sortes de parcours en largeur dans la matrice de structure (vue comme la matrice d'incidence d'un graphe d'adjacence).
```python=
# Calcule la permutation qui permet de minimiser la largeur de bande de M
import scipy.sparse.csgraph as spgraph
perm=spgraph.reverse_cuthill_mckee(M)
# Fonction qui applique la permutation sur la matrice M
M = apply_permutation(M,perm)
SLU=spl.splu(M,permc_spec="NATURAL")
occupancy(SLU.U)
```
|  |
| -------- |
| M a été réordonnée sur l'algorithme de reverse Cuthill-McKee. Structure pour la matrice L de M=LU |
Ecrivez la fonction qui applique la permutation `perm` aux éléments de la matrice creuse M. Attention, il faut suivre ces étapes:
- convertir M en une matrice COO (notée E)
- trouver la permutation `pinv` inverse à `perm`
- cette permutation change les indices à la fois des lignes et des colonnes de la matrice E. On applique donc la permutation `pinv` aux lignes et aux colonnes des coefficients non nuls de E
- refaire une matrice CSC à partir de E et la retourner
Complétez le tableau précédent avec ce mode. Que se passe-t'il si on
augmente la taille de la matrice M ? Vous tracerez aussi les temps
d'exécution de `splu` en fonction du nombre d'éléments non nuls de M.
Enfin, que se passe-t-il si vous utilisez l'algorithme de Reverse
Cuthil-McKee et que vous utilisez en plus l'heuristique de SuperLU
"COLAMD" ? Améliorez-vous les résultats ?
### IV.4 Algorithme de Cholesky dans le cas où A est symétrique.
Lorsque A est symétrique, la décomposition LU devient une décomposition $L D L^T$. Si A est de plus définie positive, les termes de la diagonales sont strictement positifs et on peut écrire $A = L L^T$. Avec un argument récursif assez simple, on montre alors qu'on peut calculer L par colonne ainsi:
- première colonne:
$$
l_{11} = \sqrt{a_{11}}, \quad l_{j1}=\frac{a_{j1}}{l_{11}}, \text{pour } j=2,\ldots,n.
$$
- autres colonnes $\forall i=2,\ldots,n$ :
$$
l_{ii} = \sqrt{a_{ii} - \sum_{k=1}^{i-1} l_{ik}^2}, \quad
l_{ji} = \frac{1}{l_{ii}}\left(a_{ji} - \sum_{k=1}^{i-1}l_{ik}l_{jk}\right), \text{ pour } j=i+1,\ldots,n.
$$
Ecrire cet algorithme de manière naïve. Pour simplifier, la matrice L de sortie sera fabriquée dense ainsi:
```python=
def CholeskyNaif( A ):
""" A est une matrice symétrique définie positive quelconque"""
n = order(A)
L = np.asmatrix( np.zeros( (n,n) ) )
...
return L
# On se fabrique une matrice symétrique définie positive ici une matrice
# classique lorsqu'on fait de la diffusion
# A = Id + 0.1 Lap
I_coo = sp.identity( 100, dtype='float' ).tocoo()
Lap_coo = gridCooMatrix( 10 )
A_coo = I_coo - 0.1 * Lap_coo
A = A_coo.tocsc()
L = CholeskyNaif( A )
print( lin.norm( A - L * L.transpose() ) )
```
Vérifiez qu'elle fonctionne en calculant la norme $\| A - L L^T \|$.
Affichez les temps de calcul. Peut-on calculer Cholesky sur une grille 100x100 (une toute petite image) ?
### IV.5 Optimisition de l'algorithme de Cholesky
Affichez la structure de A et de `CholeskyNaif(A)`. Utilisez maintenant l'algorithme de Reverse Cuthill-McKee et affichez de nouveau la structure de A et de `CholeskyNaif(A)`.
On voit que L et sa transposée ont la même enveloppe que A. On va exploiter ce fait pour limiter considérablement les boucles internes dans l'algorithme de Cholesky.
Avant de réécrire `CholeskyNaif`, on va d'abord précalculer deux tableaux F et L de taille n, qui vont représenter l'enveloppe de A. Plus précisément, la case F[i] contient la première colonne où la ligne A[i,.] n'est pas vide et L[i] contient la dernière colonne où la ligne A[i,.] n'est pas vide. Ecrivez cette fonction `enveloppe(A)` qui retourne `(F,L)`, en utilisant le fait que la matrice A en entrée est CSR.
> **Attention** il faut garantir que F et L sont des fonctions croissantes. On le fait dans la fonction `enveloppe` en faisant une deuxième passe sur F de la fin jusqu'au début et en forçant F[i-1] à avoir la valeur F[i] si elle est plus grande, et en faisant une deuxième passe sur L du début jusqu'à la fin et en forçant L[i+1] à avoir la valeur L[i] si elle est plus grande. [color=#d00000]
Vous pouvez vérifier votre fonction enveloppe ainsi
```python=
F,L=enveloppe(M)
n=order(M)
B=np.asmatrix(np.zeros( (n,n) ) )
for i in range(n):
for j in range(F[i],L[i]):
B[i,j]=1.
occupancy(B)
```
|  |  |
| -------- | -------- |
| Structure de A | Envelopppe de A |
Maintenant, pour écrire la fonction `Cholesky(A)`, qui prend en entrée une matrice CSR A, il ne reste plus qu'à reprendre la fonction `CholeskyNaif` et à modifier les bornes utilisées dans l'algorithme en tenant compte de l'enveloppe de A.
A part la boucle extérieure i, chaque fois qu'une boucle démarre à 0, on peut la faire démarrer à `F[...]`, chaque fois qu'une boucle termine à n, on peut la faire terminer à `L[...]`. Le `...` est i ou j selon le contexte.
Vérifiez que votre algorithme produit le même résultat et va (beaucoup) plus vite. On peut envisager de traiter des matrices beaucoup plus grandes qu'avec `CholeskyNaif`.
> Même si on va utiliser les caractéristiques "creuses" de A, on va néanmoins garder le fait que la matrice L fabriquée est faite sous forme dense. L'algorithme serait plus compliqué à écrire si on fabriquait en plus une matrice creuse. [color=#907bf7]