1715 views
owned this note
---
title: Sur l'épreuve pratique NSI — sujet n°3, 2022
langs: fr-fr
tags: c3i, ep
...
#  Sur l'épreuve pratique NSI — sujet n°3, 2022
> C3I : commission inter-IREM informatique
> [univ-irem.fr/c3i](https://www.univ-irem.fr/spip.php?rubrique506)
> [c3i-contact@groupes.renater.fr](mailto:c3i-contact@groupes.renater.fr)
> décembre 2022
- Thème de l'exercice 1 : codage par différence
- Thème de l'exercice 2 : représentation d'expressions arithmétiques par des arbres binaires
## Introduction
Ce document propose une analyse des deux exercices du sujet n°3 de l'épreuve pratique de Numériques et sciences informatiques (NSI) du baccalauréat 2022. Nous proposons pour chaque exercice une transcription de l'énoncé, des solutions possibles, une analyse des notions en jeu et de leur présentation dans l'exercice, des suggestions éventuelles d'énoncés alternatifs.
## Exercice 1
**Mots-clés :** tableaux ou listes, parcours linéaire, accumulation, calculs numériques
### Énoncé
:::info
EXERCICE 1 (4 points)
Le codage par différence (_delta encoding_ en anglais) permet de compresser un tableau de données en indiquant pour chaque donnée, sa différence avec la précédente (plutôt que la donnée elle-même). On se retrouve alors avec un tableau de données assez petites nécessitant moins de place en mémoire. Cette méthode se révèle efficace lorsque les valeurs consécutives sont proches.
Programmer la fonction `delta` qui prend en paramètre un tableau non vide de nombres entiers et qui renvoie un tableau contenant les valeurs entières compressées à l'aide cette technique.
Exemples :
```python=
>>> delta([1000, 800, 802, 1000, 1003])
[1000, -200, 2, 198, 3]
>>> delta([42])
42
```
:::
### Propositions de solutions
``` python=
def delta(tab):
# Condition d'utilisation : le tableau est non vide.
acc = [tab[0]]
for i in range(1, len(tab)):
acc.append(tab[i] - tab[i-1])
return acc
```
ou, en itérant directement sur les éléments de `tab:
``` python=
def delta(tab):
# Condition d'utilisation : le tableau est non vide.
prec = tab[0] # élément précédent
acc = [prec]
for elem in tab[1:]:
acc.append(elem - prec)
prec = elem
return acc
```
Cette seconde solution semble moins convenir pour des élèves de lycée, car elle impose l'usage de la syntaxe des tranches (*slices*) et d'une variable temporaire permettant de mémoriser l'élément précédent.
### Analyse
Le thème de l'exercice (compression par différences) fournit un contexte intéressant à l'exercice. Cependant il manque un peu de précision pour être totalement vraisemblable : l'efficacité repose sur le fait qu'on puisse représenter en machine les différences en utilisant moins de mémoire que les éléments du tableau eux-mêmes (ce qui n'est en général pas le cas en Python, sauf pour de très grands nombres).
L'algorithme attendu est un parcours de tableau (liste) avec construction d'une nouvelle liste (autrement dit un *accumulateur* de type liste : une variable associée à un objet de type liste, auquel on ajoute des éléments à chaque itération).
L'exercice présente une difficulté particulière dans le fait de devoir traiter différemment le premier élément de la liste, et ne parcourir que les éléments suivants. Une autre difficulté consiste à comparer les éléments consécutifs de la liste sans commettre d'erreur d'indice.
Une pré-condition explicite sur le paramètre (« un tableau non vide de nombres entiers ») est donnée dans l'énoncé. C'est une propriété que l'on suppose vraie pour toute valeur du paramètre afin de garantir la correction du résultat. L'élève n'a donc pas besoin de vérifier dans la fonction si la liste est non vide. Il n'est pas certain que ce contrat soit très explicite dans toutes les classes de NSI, ni même pour les examinateurs de l'épreuve.
### Conclusion
La présence d'un petit texte situant le contexte de l'exercice est appréciable.
Il y a peu de chances que l'élève ait déjà écrit cette fonction (ou une fonction très ressemblante) en classe, ce qui est pourtant requis par les textes régissant l'épreuve. Pour cette raison, et du fait que le parcours est légèrement plus complexe qu'un simple parcours, on peut supposer que l'exercice est plutôt difficile.
## Exercice 2
**Mots-clés :** arbres binaires, parcours en profondeur, programmation orientée objet, modélisation d'objets mathématiques, expressions arithmétiques.
### Énoncés
Voici une première version de l'énoncé, récupérée sur le site du ministère[^men-ec3-2022] et datée du 7 janvier 2022.
:::info
EXERCICE 2 (4 points)
Une expression arithmétique ne comportant que les quatre opérations +, −,×,÷ peut être représentée sous forme d'arbre binaire. Les nœuds internes sont des opérateurs et les feuilles sont des nombres. Dans un tel arbre, la disposition des nœuds joue le rôle des parenthèses que nous connaissons bien.

En parcourant en profondeur infixe l'arbre binaire ci-dessus, on retrouve l'expression notée habituellement :
$$3 \times (8 + 7) − (2 + 1)$$
La classe `Noeud` ci-après permet d'implémenter une structure d'arbre binaire.
Compléter la fonction récursive `expression_infixe` qui prend en paramètre un objet de la classe `Noeud` et qui renvoie l'expression arithmétique représentée par l'arbre binaire passé en paramètre, sous forme d'une chaîne de caractères contenant des parenthèses.
Résultat attendu avec l'arbre ci-dessus :
```python=
>>> e = Noeud(Noeud(Noeud(None, 3, None), '*', Noeud(Noeud(None, 8, None),
'+', Noeud(None, 7, None))), '-', Noeud(Noeud(None, 2, None), '+',
Noeud(None, 1, None)))
>>> expression_infixe(e)
'((3*(8+7))-(2+1))'
```
```python=
class Noeud:
'''
Classe implémentant un noeud d'arbre binaire disposant de 3
attributs :
- valeur : la valeur de l'étiquette,
- gauche : le sous-arbre gauche.
- droit : le sous-arbre droit.
'''
def __init__(self, g, v, d):
self.gauche = g
self.valeur = v
self.droit = d
def est_une_feuille(self):
'''Renvoie True si et seulement si le noeud est une feuille'''
return self.gauche is None and self.droit is None
def expression_infixe(e):
s = ...
if e.gauche is not None:
s = s + expression_infixe(...)
s = s + ...
if ... is not None:
s = s + ...
if ...:
return s
return '('+ s +')'
```
:::
Dans une version plus récente (datée du 22 février 2022, récupérée à la même adresse[^men-ec3-2022]), la définition de la classe `Noeud` et la fonction à trous ont été modifiées ainsi :
[^men-ec3-2022]: https://eduscol.education.fr/document/33184/download
:::info
```python=
class Noeud:
'''
Classe implémentant un noeud d'arbre binaire disposant de 3
attributs :
- valeur : la valeur de l'étiquette,
- gauche : le sous-arbre gauche.
- droit : le sous-arbre droit.
'''
def __init__(self, g, v, d):
self.gauche = g
self.valeur = v
self.droit = d
def __str__(self):
return str(self.valeur)
def est_une_feuille(self):
'''Renvoie True si et seulement si le noeud est une feuille'''
return self.gauche is None and self.droit is None
def expression_infixe(e):
s = ...
if e.gauche is not None:
s = ‘(‘ + s + expression_infixe(...)
s = s + ...
if ... is not None:
s = s + ... + ...
if ... :
return s
```
:::
### Propositions de solutions
Voici une proposition de solution pour la version préliminaire du sujet :
``` python=
class Noeud:
def __init__(self, g, v, d):
self.gauche = g
self.valeur = v
self.droit = d
def est_une_feuille(self):
'''Renvoie True si et seulement si le noeud est une feuille'''
return self.gauche is None and self.droit is None
def expression_infixe(e):
s = ''
if e.gauche is not None:
s = s + expression_infixe(e.gauche)
s = s + str(e.valeur)
if e.droit is not None:
s = s + expression_infixe(e.droit)
if e.est_une_feuille():
return s
return '('+ s +')'
```
Voici une proposition de solution pour la seconde version du sujet. On remarque la condition `if True` à la ligne 28 (il faut bien remplir les `...`). Comme discuté plus loin, la condition `if e.est_une_feuille()` ne convient pas.
```python=
class Noeud:
'''
Classe implémentant un noeud d'arbre binaire disposant de 3
attributs :
- valeur : la valeur de l'étiquette,
- gauche : le sous-arbre gauche.
- droit : le sous-arbre droit.
'''
def __init__(self, g, v, d):
self.gauche = g
self.valeur = v
self.droit = d
def __str__(self):
return str(self.valeur)
def est_une_feuille(self):
'''Renvoie True si et seulement si le noeud est une feuille'''
return self.gauche is None and self.droit is None
def expression_infixe(e):
s = ''
if e.gauche is not None:
s = '(' + s + expression_infixe(e.gauche)
s = s + str(e.valeur)
if e.droit is not None:
s = s + expression_infixe(e.droit) + ')'
if True : # seule proposition possible pour répondre à l'énnoncé
return s
```
### Analyse
Les arbres syntaxiques d'expressions algébriques ne sont pas explicitement au programme de NSI, mais la notion de parcours infixe d'un arbre y figure.
#### Parenthésage des expressions
Il est intéressant de remarquer que l'expression arithmétique $3 \times (8 + 7) − (2 + 1)$ donnée en. exemple dans le corps de l'énoncé n'est pas parenthésée de la même manière que l'exemple de résultat $\left((3 \times (8 + 7)) − (2 + 1)\right)$ de la fonction, ce qui peut entraîner de la confusion. En effet, écrire une fonction qui omet les parenthèses redondantes selon les règles de priorité usuelles est une tâche beaucoup plus difficile.
L'énoncé prend néanmoins la peine de qualifier cet exemple « [d]'expression notée habituellement », distinguant ainsi l'objet lui-même de ses écritures.
#### Sur la notion d'arbre binaire
La notion appropriée d'arbre binaire est sujette à de nombreux débats dans la communauté des enseignants du secondaire. Plusieurs définitions possibles d'usages variés existant dans le savoir savant, mais les programmes de NSI ne précisent pas laquelle est visée.
Cet énoncé sous-entend que tous les nœuds internes sont binaires, or le code proposé accepte des arbres dont les nœuds peuvent avoir un seul fils, gauche ou droit, qui de plus sont considérés comme différents.
Dans la version définitive du sujet, on note que la condition finale de la fonction `expression_infixe` est mal formée : en effet quelle que soit la condition utilisée ligne 28, la fonction renvoie `None` quand cette condition est fausse. La seule condition possible semble donc être `True`, ce qui rend évidemment l'instruction conditionnelle inutile.
Plus grave, si la fonction `expression_infixe` reçoit un arbre dont un des nœuds internes a un seul fils, aucune erreur ne se produit mais il manquera nécessairement une parenthèse dans le résultat final (quelle que soit la manière dont l'élève la complète). Par exemple pour la proposition de correction fournie plus bas, voici un exemple illustrant ce problème :
```python
>>> arbre = Noeud(Noeud(None, '5', None), '+', None)
>>> expression_infixe(arbre)
'(5+'
```
La version précédente du sujet aurait renvoyé le résultat suivant :
```python
>>> arbre = Noeud(Noeud(None, '5', None), '+', None)
>>> expression_infixe(arbre)
'(5+)'
```
D'autre part, la méthode `__str__` incluse dans la classe `Noeud` n'est pas utile pour la résolution de l'exercice. Sans doute était-il envisagé de remplacer la ligne 25 par un simple `s = s + str(e)`.
Il semble que la modification du code entre les deux versions de l'énoncé a été faite hâtivement et sans être testée.
Enfin, dans ces deux versions le code suggéré ne dépend en aucun cas du fait que l'arbre représente une expression : il s'agit d'un parcours infixe d'arbre binaire en toute généralité. La notion d'arbre d'expression fait donc un peu office de prétexte dans cet exercice, et n'intervient pas dans sa résolution.
#### Sur la représentation graphique de l'arbre
La représentation imagée de l'arbre peut être questionnée. En effet, les flèches font référence à la représentation d'un graphe orienté, alors cette notion d'orientation est absente des arbres. La distinction entre les nœuds internes et les feuilles n'est pas identifiable. Une autre représentation possible, est la suivante (le code Tikz utilisé pour générer cette figure est fourni en [annexe ci-après](#Annexe-%E2%80%94-code-Tikz)
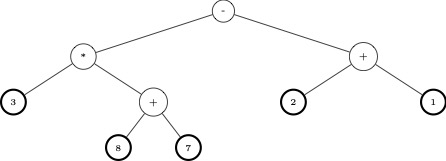
Ce type de représentation, où un nœud interne est toujours dessiné à droite de son sous-arbre gauche et à gauche de son sous-arbre droit permet aussi d'imaginer le résultat du parcours infixe comme une projection de chaque nœud sur un axe horizontal.
#### Sur l'implémentation du parcours infixe
Le parcours suggéré par le code à trous obéit à la pré-condition implicite que le paramètre `e` ne prend jamais la valeur `None`, sans quoi l'évaluation de `e.gauche` ligne 23 provoque une exception.
La fonction `expression_infixe` proposée est extérieure à la classe `Noeud` mais exploite sa structure interne, ce qui n'est généralement pas considéré comme une pratique recommandée. Il n'y aucun obstacle a priori à en faire une méthode dans le cas présent :
```python=
# dans la classe Noeud
def expression_infixe(self):
s = ''
if self.gauche is not None:
s = s + self.gauche.expression_infixe()
s = s + str(self.valeur)
if self.droit is not None:
s = s + self.droit.expression_infixe()
if self.est_une_feuille():
return s
return '('+ s +')'
```
ou encore, pour des arbres dont tous les nœuds internes sont binaires comme celui de l'exemple fourni (on dit parfois que l'arbre binaire est *localement complet*, ou _strict_) :
```python=
# dans la classe Noeud
def expression_infixe(self):
# Attention, suppose que l'arbre binaire est strict.
if self.est_une_feuille():
return str(self.valeur)
else:
expr_g = self.gauche.expression_infixe()
expr_d = self.droit.expression_infixe()
return '(' + expr_g + self.valeur + expr_d + ')'
```
Il serait nécessaire *a minima* d'indiquer explicitement par un commentaire dans la définition de la classe `Noeud` que les arbres représentés sont supposés stricts, et donc que les paramètres `g` et `d` de `__init__` sont soit tous les deux `None` (c'est une feuille), soit aucun ne l'est (c'est un nœud interne).
Il serait aussi possible de compléter la méthode `__init__` pour imposer cet invariant et lancer une exception s'il n'est pas vérifié (ce qui sort du programme de NSI).
Le fait que l'absence de fils gauche ou droit soit représentée par le fait que les attributs `gauche` et `droit` de `Noeud` valent `None` est implicite, et doit être compris par l'élève à la seule lecture de la méthode `est_une_feuille`.
### Suggestions
Voici une suggestion d'énoncé tentant de pallier à ces problèmes.
:::info
Une expression arithmétique ne comportant que les quatre opérations binaires +, −, ×, ÷ peut être représentée sous la forme d'un arbre binaire étiqueté dit *strict*, c'est-à-dire dont chaque nœud interne a exactement deux fils.
L'étiquette associée à chaque nœud interne est un caractère représentant un opérateur (`+`, `-`, `*` et `/`). L'étiquette associée à chaque feuille est un nombre (`int` ou `float`).

En effectuant un parcours en profondeur infixe de l'arbre binaire ci-dessus, on retrouve l'expression $((3*(8+7))-(2+1))$ notée habituellement :
$$3 \times (8 + 7) − (2 + 1)$$
La classe `Expression` ci-après permet d'implémenter des expressions arithmétiques représentées par des arbres binaires.
Elle permet aussi de les afficher et les évaluer.
Exemple avec l'arbre dessiné ci-dessus :
```python=
>>> expr = Expression(
... Expression(
... Expression(None, 3, None),
... '*',
... Expression(
... Expression(None, 8, None),
... '+',
... Expression(None, 7, None)
... )
... ),
... '-',
... Expression(
... Expression(None, 2, None),
... '+',
... Expression(None, 1, None)
... )
... )
>>> expr.representation_infixe()
'((3*(8+7))-(2+1))'
>>> expr.valeur()
42
```
Le code à compléter est le suivant :
```python=
class Expression:
"""
Classe implémentant une expression arithmétique
sous la forme d'un noeud d'arbre binaire strict
disposant de 3 attributs :
- etiquette : l'étiquette associée au noeud ;
- gauche : le sous-arbre gauche ;
- droit : le sous-arbre droit.
"""
def __init__(self, operande_g, op_ou_nombre, operande_d):
"""
Initialise une expression qui est
- soit un nombre ;
- soit un opérateur associé à ses deux opérandes.
Pré-conditions :
- op_ou_nombre doit être '+', '-', '*' ou '/',
ou un nombre (int ou float) ;
- operande_g et operande_d doivent être
- tous les deux des Expression si op_ou_nombre est un caractère,
- tous les deux None si c'est un nombre.
"""
self.gauche = operande_g
self.etiquette = op_ou_nombre
self.droit = operande_d
def est_une_feuille(self):
"""
Renvoie
- True si le noeud est une feuille;
- False sinon.
"""
return self.gauche is None and self.droit is None
def representation_infixe(self):
"""
Renvoie une représentation infixe complètement
parenthésée de l'expression, sous forme de str.
>>> expr1 = Expression(None, 5, None)
>>> expr1.representation_infixe()
'5'
>>> expr2 = Expression(expr1, '+', expr1)
>>> expr2.representation_infixe()
'(5+5)'
"""
if ...:
return str(self.etiquette)
else:
... = self.gauche.representation_infixe()
expr_droite = ...
return '(' + ... + self.etiquette + ... + ...
def valeur(self):
"""
Renvoie la valeur de l'expression.
>>> expr1 = Expression(None, 5, None)
>>> expr1.valeur()
5
>>> expr2 = Expression(expr1, '*', expr1)
>>> expr2.valeur()
25
"""
if self.est_une_feuille():
return ...
else:
valeur_g = ...
valeur_d = ...
if self.etiquette == '+':
return valeur_g + valeur_d
elif ...:
return valeur_g - ...
elif self.etiquette == '*':
return ...
else: # ici self.etiquette est supposé égal à '/'
return ...
```
Compléter :
1. la méthode récursive `representation_infixe` qui renvoie l'expression arithmétique représentée par l'arbre binaire passé en paramètre, sous forme d'une chaîne de caractères complètement parenthésée ;
2. la méthode récursive `valeur` qui renvoie la valeur de l'expression représentée par l'arbre binaire.
:::
#### Proposition de solution pour la suggestion
```python=
class Expression:
"""
Classe implémentant une expression arithmétique
sous la forme d'un noeud d'arbre binaire strict
disposant de 3 attributs :
- etiquette : l'étiquette associée au noeud ;
- gauche : le sous-arbre gauche ;
- droit : le sous-arbre droit.
"""
def __init__(self, operande_g, op_ou_nombre, operande_d):
"""
Initialise une expression qui est
- soit un nombre ;
- soit un opérateur associé à ses deux opérandes.
Pré-conditions :
- op_ou_nombre doit être '+', '-', '*' ou '/',
ou un nombre (int ou float) ;
- operande_g et operande_d doivent être
- tous les deux des Expression si op_ou_nombre est un caractère,
- tous les deux None si c'est un nombre.
"""
self.gauche = operande_g
self.etiquette = op_ou_nombre
self.droit = operande_d
def est_une_feuille(self):
"""
Renvoie
- True si le noeud est une feuille;
- False sinon.
"""
return self.gauche is None and self.droit is None
def representation_infixe(self):
"""
Renvoie une représentation infixe complètement
parenthésée de l'expression sous forme de str.
>>> expr1 = Expression(None, 5, None)
>>> expr1.representation_infixe()
'5'
>>> expr2 = Expression(expr1, '+', expr1)
>>> expr2.representation_infixe()
'(5+5)'
"""
if self.est_une_feuille():
return str(self.etiquette)
else:
expr_gauche = self.gauche.representation_infixe()
expr_droite = self.droit.representation_infixe()
return '(' + expr_gauche + self.etiquette + expr_droite + ')'
def valeur(self):
"""
Renvoie la valeur de l'expression.
>>> expr1 = Expression(None, 5, None)
>>> expr1.valeur()
5
>>> expr2 = Expression(expr1, '*', expr1)
>>> expr2.valeur()
25
"""
if self.est_une_feuille():
return self.etiquette
else:
valeur_g = self.gauche.valeur()
valeur_d = self.droit.valeur()
if self.etiquette == '+':
return valeur_g + valeur_d
elif self.etiquette == '-':
return valeur_g - valeur_d
elif self.etiquette == '*':
return valeur_g * valeur_d
else: # ici self.etiquette est supposé égal à '/'
return valeur_g / valeur_d
```
### Conclusion
Le thème de la représentation d'une expression algébrique par un arbre est intéressant et pertinent en classe de terminale.
Cet exercice nous semble cependant problématique dans le contexte de l'enseignement de NSI et plus encore dans le contexte de l'épreuve pratique de baccalauréat.
Dans un exercice de type « code à trous », dont nous ne discutons pas ici le bien-fondé pédagogique, il nous semble crucial que le code à compléter soit aussi clair et compréhensible que possible, et si possible dépourvu d'erreurs. Nous avons relevé dans l'énoncé officiel plusieurs ambiguités relatives à la définition des arbres binaires et à la pertinence de la modélisation proposée.
D'autre part, il semble que des versions successives du sujet aient été élaborées, et que des erreurs ou imprécisions supplémentaires aient été introduites à l'occasion de sa révision.
## Annexe — code Tikz
```latex
\documentclass{standalone}
\usepackage{tikz}
\usetikzlibrary{trees}
\begin{document}
\begin{tikzpicture}[
scale=0.7,
level distance=1.3cm,
level 1/.style={sibling distance=8cm},
level 2/.style={sibling distance=4cm},
level 3/.style={sibling distance=2cm},
level 4/.style={sibling distance=1cm},
level 5/.style={sibling distance=0.5cm}]
\tikzstyle{every node}=[circle,draw,font=\fontsize{4}{0}\selectfont
]
\node (Root) {-}
child{
node {*}
child{
node[very thick] {3}
}
child{
node{+}
child{
node[very thick]{8}
}
child{
node[very thick]{7}
}
}
}
child{
node {+}
child{
node[very thick]{2}
}
child{
node[very thick]{1}
}
}
;
\end{tikzpicture}
\end{document}
```