Stages Recherche ANR StableProxies === ## Contexte In many applicative areas such as engineering, numerical simulations, fabrication, or material sciences, modeling geometrical objects and performing numerical analysis have become the cornerstone of many design processes or decision-making strategies. The aim of the StableProxies project is to provide high-performance and stable geometry processing tools to perform reliable numerical computations on generic geometrical objects. In the project, we address a large class of discrete geometrical structures that may be used for the simulation of physical phenomena. Depending on the acquisition or design process, and on the application constraints, various data structures coexist to describe 3D shapes. Discrete meshes approximate surfaces using piecewise linear or higher order elements with sometimes incorrect topological information. They are widely used in engineering and computer graphics (see Fig(a-b)).  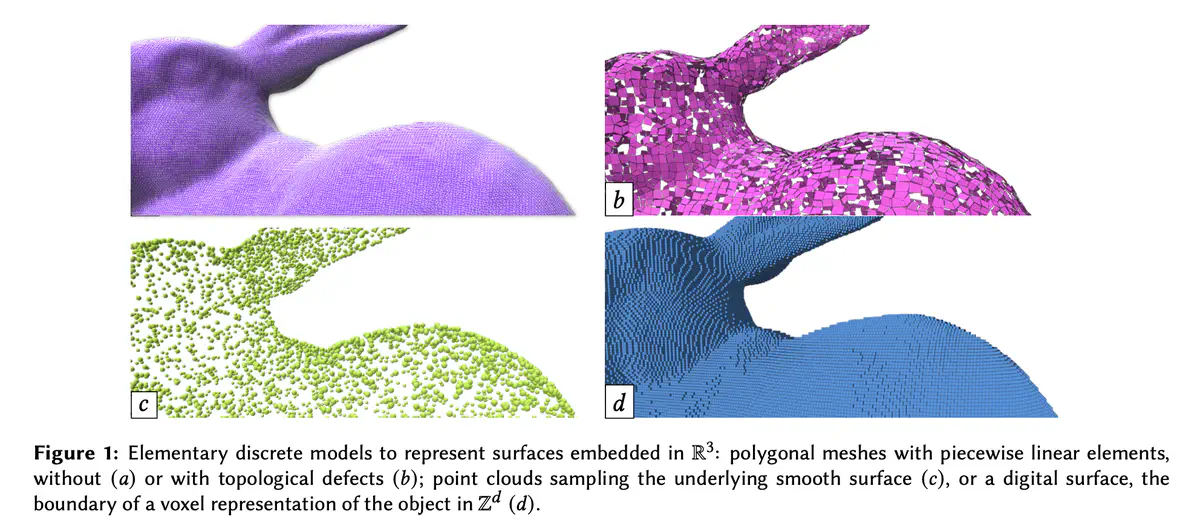The main overall objective of the StableProxies project is to provide **theoretically stable and efficient tools to perform high-performance geometric computations on complex, heterogeneous and defective discrete geometrical data.** We claim that the digital model (subsets of $\mathbb{Z}^𝑑$, or subsets of the cellular decomposition of $\mathbb{Z}^𝑑$) is a good candidate for high-performance and reliable geometrical computations. We aim at developing robust geometry processing tools using a **digital proxy model.** :::warning **Location:** LIRIS lab, [Univ Lyon1 campus](https://liris.cnrs.fr/presentation/pour-acceder-luniversite-claude-bernard-lyon1) **Required skills**: computer graphics, geometry, applied math, c++/python programming. ::: ## Subject 1: Continuous maps between heterogeneous data (point cloud, meshes) and digital proxies As mentioned above, the goal of the Stable Proxies project is to be able to run numerical simulations on heterogeneous data : the input data can be point clouds, voxels or surface meshes, sometimes faulty with outliers (points resulting from measurement errors during an acquisition process for instance) or connectivity issues (cracks in the surface, self-intersections for instance). Numerical simulations on the contrary require nicely meshed domains : triangle or tetrahedral meshes for finite elements, with requirements on the shape of the triangles to ensure the convergence of the simulation, or even regular grids. Our goal is therefore to design a proxy object matching the quality requirements to run numerical simulations, but also closely related to the input faulty data. We also need a mapping to transfer attributes from the input data to the proxy to initialize the simulation, and back to recover the result of the simulation. This subject aims at both constructing the proxy and defining its mapping with the input data. The designed proxy has to be suitable for numerical simulations and to accurately match the input data in terms of position, normal vectors and curvatures. As mentioned above, a digital model could be a suitable choice of proxy [^CalculusDigitalSurfaces]. Designing the correct digital model for a given input data remains a challenge, in particular to automatically detect the dimensionality of the input data and use a grid resolution accurate enough for the input data but also tractable in terms of numerical simulation. Remeshing for simulation is still an active field of research [^HexMesh] and handling mesh quality is one of the most challenging problems of the field. A closely related approach for instance is the polycube maps approach mapping the input data to a subset of $\mathbb{Z}^𝑑$  Image courtesy of C.Dumery et al. [^Evocube] <!-- TODO : élaborer plus sur le transport optimal fournir des références --> When mapping between the proxy and the input data, classical *baking* techniques usually use the nearest point interpolation or matching parameterizations of both the source and target. Parameterization can be a challenging problem on faulty data and the nearest point interpolation can lead to artifacts : attributes being mapped to several parts of the target object, or attributes of the input object not mapped to anything on the target. Designing maps between shapes is a classical problem in computer graphics [^FunctionalMaps], [^ContinuousMaps]. Another possible research track could be the use of optimal transport (e.g. [^OT]) to ensure that all the input samples are mapped to the target with a resolution matching that of the input sampling. This would involve discrete-discrete optimal transport algorithms for instance when approximating a point cloud with a voxel proxy with a limited number of corrected normals. Semi-discrete algorithms will also be considered when building a proxy from non-manifold surfaces (like soup of triangles). Optimal setting of the normal vector field for a given proxy voxel geometry could also be considered. While building a mapping, an important challenge would be to keep track of topological properties, or inferred topological properties (e.g., dimension inference). ## Subject 2: Multigrid intrinsic solver for digital surfaces When solving a complex variational problem on large domains, multigrid solvers define a wide range of methods to efficiently solve the problem on low-resolution domains, with prolongation operators to the finer resolutions. For structured domains (grids), many solutions exist [^13]. Many geometry processing problems can be cast as positive (semi-)definite problems on discrete surfaces (parameterization, geodesics, fairing. . . ). For manifold meshes, recent approaches aim to define Galerkin geometric multigrid solvers that can be used as a black box to solve linear problems [^59]. For digital surfaces, the defective embedding of the geometry makes such intrinsic Galerkin scheme not optimal. On the other hand, trivial multigrid schemes exist for the grid supporting the digital surface definition. The objective of this task is to propose a new intrinsic-ambient multigrid solver for the high performance geometry processing on digital surfaces. As depicted in the following Figure  one way to address the problem would be to construct a multigrid scheme (and its prolongation operator) that would be consistent with the digital surface of the underlying object on the upscaled/downscaled grids. In this task, adaptive resolution representation of digital surfaces will also be investigated with the objective of designing efficient numerical solvers for solving PDE on surfaces. For instance, following [^27][^28], can a complete corrected discrete calculus on adaptive digital surfaces be designed while preserving the accuracy of the computations? ## References [^CalculusDigitalSurfaces]: David Coeurjolly, Jacques-Olivier Lachaud. A Simple Discrete Calculus for Digital Surfaces. Second International Conference on Discrete Geometry and Mathematical Morphology, Oct 2022, Strasbourg, France. ⟨hal-03719330⟩ [^volfit]: G.-P. Paillé, P. Poulin and B. Lévy. Fitting Polynomial Volumes to Surfaces Meshes with Voronoi Squared Distance Minimization. Computer Graphics Forum, 32(5):103-112, 2023 [^13]: A. Brandt. Multi-level adaptive solutions to boundary-value problems. Mathematics of computation, 31(138):333–390, 1977. [^59]: H.-T. D. Liu, J. E. Zhang, M. Ben-Chen, and A. Jacobson. Surface multigrid via intrinsic prolongation. ACM Trans. Graph., 40(4), 2021. [^27]: F. De Goes, A. Butts, and M. Desbrun. Discrete differential operators on polygonal meshes. ACM Transactions on Graphics (TOG), 39(4):110–1, 2020. [^28]: David Coeurjolly, Jacques-Olivier Lachaud. A Simple Discrete Calculus for Digital Surfaces. IAPR Second International Conference on Discrete Geometry and Mathematical Morphology October 2022 [^OT]: Gabriel Peyré, Marco Cuturi, Computational Optimal Transport, https://arxiv.org/abs/1803.00567 [^FunctionalMaps]: Ovsjanikov, Maks & Ben-Chen, Mirela & Solomon, Justin & Butscher, Adrian & Guibas, Leonidas. (2012). Functional Maps: A Flexible Representation of Maps Between Shapes. ACM Transactions on Graphics - TOG. 31. 10.1145/2185520.2185526. [^ContinuousMaps]: Corman, E., Ovsjanikov, M. and Chambolle, A. (2015), Continuous Matching via Vector Field Flow. Computer Graphics Forum, 34: 129-139. https://doi.org/10.1111/cgf.12702 [^HexMesh]: Nico Pietroni, Marcel Campen, Alla Sheffer, Gianmarco Cherchi, David Bommes, Xifeng Gao, Riccardo Scateni, Franck Ledoux, Jean Remacle, and Marco Livesu. 2022. Hex-Mesh Generation and Processing: A Survey. ACM Trans. Graph. 42, 2, Article 16 (April 2023), 44 pages. https://doi.org/10.1145/3554920 [^Evocube]: Dumery, C., Protais, F., Mestrallet, S., Bourcier, C. and Ledoux, F. (2022), Evocube: A Genetic Labelling Framework for Polycube-Maps. Computer Graphics Forum, 41: 467-479. https://doi.org/10.1111/cgf.14649