---
title: Inférence bayesienne et classification dans les réseaux
---
Inférence bayesienne et classification dans les réseaux
===
> [name=Jacques-Olivier Lachaud][time=Novembre 2023][color=#907bf7]
[TOC]
## Introduction
:::info
==Inférence Bayésienne== Méthode statistique qui utilise la relation de Bayes pour mettre à jour la probabilité d'une *hypothèse* $H$ en fonction de nouvelles données $E$, appelées *évidences* en anglais.
:::
**Utilisations** Analyse dynamique d'une séquence de données, car la formulation permet la mise à jour progressive de la loi $H$, en fonction de nouvelles évidences/données.
**Applications** Science, médecine, loi, sport, ingénierie, apprentissage automatique ...
**Intérêts** La formulation permet de mettre à jour des hypothèses de loi continues ou discrètes en fonction de données quelconques (souvent discrètes).
**Prérequis** Compréhension générales des [probabilités](https://fr.wikipedia.org/wiki/Théorie_des_probabilités), notamment les [probabilités discrètes](https://fr.wikipedia.org/wiki/Variable_aléatoire_discrète) (e.g. les jeux de dés) et les [probabilités à densité](https://fr.wikipedia.org/wiki/Variable_aléatoire_à_densité) (e.g. la loi normale).
## Règle de Bayes
:::success
$$P(H | E) = \frac{P(H)P(E | H)}{P(E)}$$
:::
- $H$ est une hypothèse (loi de probabilité) dont les paramètres peuvent être affectés par les données
- $E$ correspond à de nouvelles données/observations (*evidences* en anglais) dont $H$ ne tient pas encore compte
- $P(H)$ est la probabilité de l'hypothèse a priori (**prior**) sans tenir compte de $E$.
- $P(H| E)$ est la probabilité postérieure (**posterior**), c'est-à-dire la probabilité $H$ connaissant $E$. C'est ce qe l'on cherche à calculer.
- $P(E | H)$ est la probabilité d'observer $E$ en supposant $H$ et est appelé **vraisemblance** (**likelyhood**). Vu comme une fonction de $E$ avec $H$ fixe, il donne la compatibilité de l'évidence avec l'hypothèse actuel.
- $P(E)$ est la probabilité des données a priori (**model evidence** ou **marginal likelyhood**).
==Preuve== Par définition des probabilités conditionnelles, $P(H \cap E )= P(H | E)P(E)$ et $P(E \cap H) =P(E|H) P(H)$, or ces 2 valeurs sont identiques.
### Exemples d'utilisation de la règle de Bayes
==Exemple 1==
On cherche à déterminer la probabilité conditionnelle d'être astigmate, sachant que la personne est barbue. Soit $A=H$ l'hypothèse, $B=E$ les données. On cherche donc $P(A|B)$. On connait à l'inverse la probabilité qu'une personne soit barbue $P(B)=8/20$ et, parmi les astigmates, on connait la proportion de barbus $P(B|A)=2/5$. Enfin, on connait la proportion d'astigmate $P(A)=5/20$. On vérifie que
$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}=\frac{\frac{2}{5}\frac{5}{20}}{\frac{8}{20}} = \frac{1}{4}$$
Comme $P(A|B)=P(B)=1/4$ être astigmate est *indépendant* d'être barbu.
| | barbu $B$ | non barbu $\bar{B}$ | total |
| ----------------------- | ------------------- | ------------------------ | ------------ |
| astigmate $A$ | $P(A\cap B)$ | $P(A \cap \bar{B})$ | $P(A)$ |
| non astigmate $\bar{A}$ | $P(\bar{A} \cap B)$ | $P(\bar{A}\cap \bar{B})$ | $P(\bar{A})$ |
| total | $P(B)$ | $P(\bar{B})$ | 1 |
| Column 1 | Column 3 |
| -------------------------------------------------------------------------------------------- | -------- |
| [By Cmglee - Own work, CC BY-SA 3.0](https://commons.wikimedia.org/w/index.php?curid=33268427) |  |
Si on connait directement $P(A\cap B)$ (comme ici), on peut directement calculer avec $P(A|B)=P(A\cap B)/P(B)=2/20/(8/20)=1/4$.
==Exemple 2==
Un médecin effectue le dépistage d'une maladie à l'aide d'un test fourni par un laboratoire.
Le test donne un résultat booléen : soit positif, soit négatif. Les études sur des groupes tests ont montré que, lorsque le patient est porteur de la maladie, le test est positif dans 90 % des cas. Pour un patient non atteint de la maladie, le test est positif dans un cas sur 1000 (faux positif).
Le médecin reçoit un résultat positif pour le test d'un patient. Il souhaiterait savoir quelle est la probabilité **postérieure** que le patient soit réellement atteint de la maladie.
**Formalisation**:
- $M$ l'événement « le patient est atteint de la maladie » ($\bar{M}$ pas malade)
- $T$ l'événement « le test est positif » ($\bar{T}$ négatif)
- on cherche $P(M | T)$
- on connait les **vraisemblances** $P(T|M)=0.9$, ainsi que $P(T|\bar{M})=0.001$.
On note $p(M)=x$ la probabilité d'être malade. On évalue
$$P(T)=P(T\cap M)+P(T\cap\bar{M})=P(T|M)P(M)+P(T|\bar{M})P(\bar{M}) \Leftrightarrow P(T)=0.9x+0.001(1-x)$$
D'après la règle de Bayes,
$$P(M|T)=\frac{P(T|M)P(M)}{P(T)}=\frac{0.9x}{0.9x+0.001(1-x)}=\frac{0.9x}{0.899x+0.001}$$
En fonction de la proportion de malades dans la population, ce test peut être un bon indicateur ou un indicateur très médiocre :
| proportion malades $x$ | $1/100000$ | $1/10000$ | $1/1000$ | $1/100$ |
| ---------------------- | ---------- | --------- | --- | --- |
| probabilité d'être malade si test positif | 0,89% | 8,26% | 47,39% | 90,09% |
## Utilisation en inférence sur des modèles possibles
On peut utiliser les évidences/données pour mettre à jour la plausibilité d'un ensemble de modèles exclusifs (et exhaustifs). L'**inférence bayésienne** peut être vu comme une opération sur la distribution des plausibilités.
### Formulation générale
On suppose qu'on a un processus qui génère des événements indépendants et identiquement distribués (iid) $E_1, \ldots, E_n$, dont la distribution de probabilité est inconnue. On se donne une liste $M_1,\ldots,M_n$ de modèles possibles, vus comme des événements. Les probabilités conditionnelles $P(E_i|M_k)$ sont spécifiés et définissent le modèle. $P(M_k)$ est la **croyance** dans le modèle $M_k$ et on se donne une croyance initiale pour chaque $M_k$ avant toute inférence, avec $\sum_k P(M_k)=1$.
Si le processus génère un événement $E \in \{E_k\}$, pour chaque $M \in \{M_m\}$, on peut mettre à jour sa **probabilité a priori** $P(M_m)$ par sa **probabilité postérieure** $P(M_m|E)$. D'après la règle de Bayes
\begin{align}
\tag{1}
\forall m, P(M_m | E) = \frac{P(E | M_m)P(M_m)}{\sum_i P(E | M_i)P(M_i)}
\end{align}
Si de nouvelles données arrivent, on met à jour $P(M_k)$ en fonction.
:::success
L'hypothèse d'indépendance fait que l'ordre dans lequel arrivent les événéments n'influent pas sur le résultat.
:::
- [Exemple d'inférence bayésienne pour identifier un modèle de données](https://codimd.math.cnrs.fr/s/xAj_FhhVu)
### Formulation à partir d'observations multiples
Pour une séquence d'observations iid $\mathbf{E}=(e_1,\ldots,e_k)$, on montre par induction que l'utilisation répétée de (1) conduit à la formule:
\begin{align}
\tag{2}
\forall m, P(M_m | \mathbf{E}) = \frac{P(\mathbf{E} | M_k)}{\sum_i P(\mathbf{E} | M_i)P(M_i)}P(M_m)
\end{align}
avec $P(\mathbf{E}|M_m)=\Pi_{j=1}^k P(e_j|M_m)$.
:::info
==Preuve==
Prenons par exemple deux événements $e_1,e_2$.
\begin{align}
P(M_m | e_1,e_2) & = \frac{P(e_1,e_2 | M_m)}{P(e_1,e_2)}P(M_m) \qquad \text{(en appliquant Bayes)} \\
& = \frac{P(e_1|e_2,M_m)P(e_2|M)}{P(e_1,e_2)}P(M_m) \qquad \text{(par définition de prob. cond.)}\\
& = \frac{P(e_1|M_m)P(e_2|M_m)}{\sum_i P(e_1,e_2|M_i)P(M_i)}P(M_m) \qquad \text{(car événements iid)}\\
& = \frac{P(e_1|M_m)P(e_2|M_m)}{\sum_i P(e_1|M_i)P(e_2|M_i)P(M_i)}P(M_m). \qquad \text{(car événements iid)}
\end{align}
:::
:::success
Dit autrement, on peut aussi mettre à jour les probabilités du modèle en prenant les observations paquets par paquets.
:::
### Formulation paramétrique
On peut aller un cran plus loin en considérant un nombre infini de modèles. On considère alors une famille de modèles $M(\theta)$ où $\theta$ désigne un ensemble de paramètres possibles (e.g. $\theta$ peut être un réel, ou un vecteur de réels). Dans ce cas, on note simplement $\theta$ pour désigner un modèle et $p(\theta)$ est sa [densité de probabilité](https://fr.wikipedia.org/wiki/Variable_aléatoire_à_densité).
\begin{align}
\tag{3}
\forall \theta, p(\theta | \mathbf{E}) = \frac{p(\mathbf{E} | \theta)}{\int p(\mathbf{E} | \theta)p(\theta) d\theta}p(\theta).
\end{align}
avec $p(\mathbf{E}|\theta)=\Pi_{j=1}^k p(e_j|\theta)$.
:::success
L'inférence bayésienne fait donc évoluer toute la distribution de probabilités du modèle à chaque (groupe d') observation(s).
:::
:::warning
On note le passage de probabilités d'événements discrets $P(\cdot)$ à des densités de probabilités sur des ensembles mesurables $p(\cdot)$. Au dénominateur, on mesure donc la probabilité $p(\mathbf{E})$ en intégrant $p(\mathbf{E}|\theta)p(\theta)$ sur tous les $\theta$ possibles. Au numérateur, le $\theta$ est choisi.
:::
:::danger
Très souvent, en apprentissage automatique, il n'est pas possible de calculer sur tous les $\theta$ possibles, et on fait des approximations. Dans certains cas, on peut calculer analytiquement les intégrales.
:::
==Exemple== [Inférence bayésienne paramétrique pour résoudre le problème "Birth sex ratio" (Laplace, 1786)](https://codimd.math.cnrs.fr/s/5G_NKdUH5)
## Inférence Bayésienne générale
- $x$ est une donnée, qui peut être aussi un vecteur
- $\theta$ est un vecteur de paramètres du modèle, donc $x$ suit la loi $p(x | \theta)$
- $\alpha$ le vecteur des hyper-paramètres, donc $\theta \sim p(\theta | \alpha )$.
- $\mathbf{X}$ les données observées $x_{1},\ldots ,x_{n}$
- ${\widetilde {x}}$ une nouvelle donnée dont la distribution veut être prédite.
### Probabilités considérées et inférence bayésienne
- $p(\theta|\alpha)$ est la **distribution a priori**, ou **prior**, des paramètres du modèle, pas toujours facile à déterminer. On les suppose parfois équiprobables. En apprentissage automatique, on pénalise souvent les grandes valeurs en les rendant peu probables, par exemple $p(\theta|\alpha) \sim \mathcal{N}(0,\sigma^2)$ et $\sigma \in \alpha$ est un hyper-paramètre.
- $p(\mathbf{X}|\theta)$ est la **distribution d'échantillonnage** ou **vraisemblance** d'avoir ces données en fonction des paramètres du modèle.
- $p(\mathbf{X}|\alpha)$ est l'**évidence** ou **distribution marginale** (c'est-à-dire indépendante des autres, dans les marges). On peut l'obtenir ainsi
$$p(\mathbf{X}|\alpha) = \int p(\mathbf{X}|\theta,\alpha)p(\theta|\alpha)d\theta.$$
- $p(\theta|\mathbf{X},\alpha)$ est la **distribution a posteriori** ou **posterior**, une fois qu'on a tenu compte des observations $\mathbf{X}$, et on la calcule via la règle de Bayes comme ci-dessus
\begin{align}
\tag{4}
p(\theta | \mathbf{X},\alpha) = \frac{p(\theta,\mathbf{X},\alpha)}{p(\mathbf{X},\alpha)}=\frac{p(\mathbf{X} | \theta, \alpha)}{\int p(\mathbf{X} | \theta,\alpha)p(\theta|\alpha) d\theta}p(\theta|\alpha) \propto \underbrace{p(\mathbf{X} | \theta, \alpha)}_{\text{vraisemblance}} \underbrace{p(\theta|\alpha)}_{\text{a priori}}
\end{align}
avec $p(\mathbf{X}|\theta,\alpha)=\Pi_{j=1}^n p(x_j|\theta,\alpha)$.
:::info
En anglais "posterior is proportional to likelihood times prior", ou "posterior = likelihood times prior, over evidence".
:::
## Prédiction ou estimation bayésienne
- La **distribution prédite a priori** est la distribution d'un nouveau point, marginalisé sur la distribution a priori:
\begin{align}
p({\widetilde {x}}\mid \alpha )=\int p({\widetilde {x}}\mid \theta,\alpha )p(\theta \mid \alpha ) \,d\theta.
\end{align}
- La **distribution prédite a posteriori** est la distribution d'un nouveau point, marginalisé sur la distribution a priori:
\begin{align}
p({\widetilde {x}}\mid \mathbf {X} ,\alpha )=\int p({\widetilde {x}}\mid \theta,\alpha )p(\theta \mid \mathbf {X} ,\alpha )\, d\theta.
\end{align}
L'**inférence prédictive bayésienne** propose de prédire la probabilité (ou densité de probabilité) d'une nouvelle donnée en utilisation la prédiction a posterior, plutôt que de prédire un seul point. Si on peut analyser cette distribution, on peut déterminer l'incertitude d'une prédiction.
## Propriétés asymptotiques de l'inférence bayésienne
:::success
Le [théorème de Bernstein -- von Mises](https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Bernstein-von_Mises) stipule que, sous certaines hypothèses, la distribution a posteriori se concentre asymptotiquement autour du paramètre à estimer indépendamment de la distribution a priori sous un nombre suffisamment grand d'observations. Recentrée, elle tend vers une loi normale multivariée dont la matrice de covariance est l'inverse de l'[information de Fisher](https://fr.wikipedia.org/wiki/Information_de_Fisher).
En termes simples, cela veut dire que la statistique bayésienne est équivalente à l'approche [statistique classique](https://fr.wikipedia.org/wiki/Statistique), parfois appelée fréquentiste (e.g. moyenne, moments, variance, test du $\chi^2$).
:::
## Maximum a posteriori
On cherche souvent à estimer un seul modèle probable à partir de la distribution prédite a posteriori. On peut parfois calculer l'espérance de $\theta$ (i.e. sa moyenne), ou se servir de propriétés statistiques de la distribution comme ses moments. Un estimateur simple est de choisir un $\theta_{MAP}$ qui maximise la probabilité a posteriori. S'il existe, on parle de l'**estimateur maximum a posteriori**:
\begin{align}
\tag{5}
\theta_{MAP} & \in \arg\max_{\theta} p(\theta | \mathbf{X},\alpha) \\
& = \arg\max_{\theta} \underbrace{p(\mathbf{X} | \theta, \alpha)}_{\text{vraisemblance}} \underbrace{p(\theta|\alpha)}_{\text{a priori}}, \qquad(\text{le dénominateur ne change pas le max})\\
& = \arg\max_{\theta} \left[ \ln( p(\mathbf{X} | \theta,\alpha ) )+ \ln p(\theta|\alpha) \right] \qquad \text{(le logarithme n'influe pas le max)}\\
& = \arg\max_{\theta} \left[ \ln\left( \prod_{i=1}^n p( x_i | \theta,\alpha ) \right)+ \ln p(\theta|\alpha) \right] \qquad \text{(les données sont iid)}\\
\tag{6}
& = \arg\max_{\theta} \left[ \left( \sum_{i=1}^n \ln p( x_i | \theta,\alpha ) \right)+ \ln p(\theta|\alpha) \right] \quad\text{(le log transforme $\times$ en $+$)}
\end{align}
Trouver le maximum a posteriori revient donc à trouver l'optimum d'une somme de fonctions de $\theta$. On verra que c'est plus simple que de trouver l'optimum d'un produit.
On peut noter $\ell_{MAP}(\theta) := - \left[ \left( \sum_{i} \ln p( x_i | \theta,\alpha ) \right)+ \ln(p(\theta|\alpha) \right]$ le négatif de la fonction précédente, fonction coût que l'on cherche alors à **minimiser**.
## Lien avec le maximum de vraisemblance
On rappelle que la **vraisemblance** est $p(\mathbf{X}|\theta)$. Si on suppose les $n$ données iid, cette vraisemblance, souvent notée curieusement $L_n(\theta;\mathbf{X})$ s'écrit comme le produit
\begin{align}
\tag{7}
L_n(\theta;\mathbf{X}) = p(\mathbf{X}|\theta) = p(x_1 | \theta)p(x_2 | \theta) \cdots p(x_n | \theta)
\end{align}
:::spoiler
On note que $p(x|\theta)$ s'interprète de deux façons, dans le cas fini ou continue:
- si on étudie une variable aléatoire réelle discrète $X$ de paramètre $\theta$ inconnu, $p(x|\theta)=P_\theta(X=x)$,
- et si on étudie une variable aléatoire réelle continue, alors $p(x|\theta)=f_\theta(x)$
:::
Un **estimateur du maximum de vraisemblance** constitue à chercher le paramètre $\theta_{MV}$ qui maximise la quantité $L_n(\theta;\mathbf{X})$ :
\begin{align}
\tag{8}
\theta_{MV} \in \arg\max_{\theta} L_n(\theta;\mathbf{X}) &= \arg\max_{\theta} {p(\mathbf{X} | \theta)} \\
\tag{9}
& = \arg\max_{\theta} \prod_{i=1}^n p(x_i | \theta)\\
\tag{10}
& = \arg\max_{\theta} \sum_{i=1}^n \ln p(x_i | \theta).
\end{align}
Le passage de (9) à (10) vient du fait que, comme la fonction **logarithme** est croissante, les deux maximas coïncident. On verra ci-dessous qu'il est souvent beaucoup plus facile de trouver le maximum d'une somme, que le maximum d'un produit.
On peut noter $\ell_{MV}(\theta) := - \left[ \left( \sum_{i} \ln p( x_i | \theta,\alpha ) \right) \right]$ le négatif de la fonction précédente, fonction coût que l'on cherche alors à **minimiser**.
:::success
Le **maximum de vraissemblance** est un cas particulier du **maximum a posteriori**, où la **distribution a priori est supposée uniforme** (voir (5) et (8)).
:::spoiler
Il y a un petit détail technique lorsque le domaine de $\theta$ n'est pas bornée, car il n'y a alors pas de distribution uniforme. En réalité il suffit d'imaginer qu'il s'agit d'une loi normale dont la variance tend vers l'infini.
:::
## Calcul du maximum de vraissemblance et du maximum a posteriori
Si le modèle recherché est paramétré par des paramètres $\theta$ continus, alors on sait que le minimum $\theta^*$ d'une fonction de plusieurs variables doit satisfaire 2 conditions nécessaires:
- $\nabla_\theta \ell (\theta^*;\mathbf{X}) = \mathbf{0}$ : les dérivées partielles par rapport à chaque $\theta_i$ sont nulles en $\theta^*$.
- $\nabla^2_\theta \ell (\theta^*;\mathbf{X})$ est définie positive : la matrice des dérivées secondes (hessien $H_\theta$) indique une fonction convexe, i.e. $\forall \mathbf{y}, \mathbf{y}^T H_{\theta^*} \mathbf{y} \ge 0$.
:::info
Si $\theta$ est un paramètre réel (et non un vecteur), alors les conditions nécessaires sont simplement:
- $\frac{d \ell}{d \theta}(\theta^*;\mathbf{X})=0$ et $\frac{d^2 \ell}{d \theta^2}(\theta^*;\mathbf{X})\le0$.
:::
==Exemple 1==
On observe les issues d'un jeu à pile ou face et on essaie de déterminer si la pièce utilisée est biaisée dans un sens ou dans l'autre. Soit $q$ la probabilité que le dé tombe sur pile (mettons 1) et donc $1-q$ que le dé tombe sur face (mettons 0). La suite d'événements observés est une séquence $\mathbf{X}=(x_1, \ldots, x_n)$ avec $x_i \in \{0,1\}$.
On a $p(x_i=1|q) = q$ et $(p_i=0|q)=1-q$, que l'on peut résumer ainsi :
$$
p(x_i|q)=q^{x_i} (1-q)^{1-x_i} \qquad \text{(on reconnait une loi de Bernouilli)}
$$
La vraissemblance du modèle en $q$ est
\begin{align}
L_n(q;\mathbf{X}) = p(x_1 | q)\cdots p(x_n | q) = q^{x_1 + \cdots + x_n}(1-q)^{n-(x_1 + \cdots + x_n)}
\end{align}
Et on prend le négatif du logarithme de la vraisemblance car son minimum est le maximum de vraisemblance
\begin{align}
\ell(q) := -\ln \ell(q;\mathbf{X}) = -(x_1 + \cdots + x_n) (\ln q) - (n - (x_1 + \cdots + x_n))\ln (1-q)).
\end{align}
La condition nécessaire indique de vérifier où la dérivée de $l_n$ s'annule:
\begin{align}
\frac{d \ell}{d q}= -(x_1 + \cdots + x_n)\left(\frac{1}{q}+\frac{1}{1-q}\right) + \frac{n}{1-q}= \frac{qn -(x_1 + \cdots + x_n) }{q(1-q)}\\
\frac{d \ell}{d q}=0 \quad \Leftrightarrow \quad \frac{x_1 + \cdots + x_n -qn}{q(1-q)} = 0 \quad \Leftrightarrow \quad q=\frac{1}{n}\sum_{i=1}^n x_i
\end{align}
On retrouve le fait que la moyenne empirique des résultats donne le biais du dé. On peut vérifier que la dérivée seconde est positive :
\begin{align}
\frac{d^2 \ell}{d q^2} = \frac{x_1 + \cdots + x_n}{q^2} + \frac{1-(x_1 + \cdots + x_n)}{(1-q)^2} > 0.
\end{align}
# Régression logistique et classification bayésienne
## Régression logistique
En statistique, le **modèle logistique** (logit model) est un modèle statistique qui représente la probabilité de survenue d'un événement, tel que son logarithme est une combinaison linéaire d'une ou plusieurs variables indépendantes. La **régression logistique** (ou régression logit) est le fait d'estimer les paramètres du modèle logistique (les coefficients de la combinaison linéaire).
Ces modèles sont très souvent utilisés pour décider si une donnée appartient à une classe (décision 0 ou 1) ou pour décider si une donnée appartient à une classe parmi $n$.
### Modèle logistique
Le modèle se base sur la fonction logistique $p(x)=\frac{1}{1+e^{-(x-\mu)/s}}$. Le paramètre $\mu$ désigne l'endroit où la fonction vaut $1/2$, $s$ est un paramètre d'échelle qui dilate ou contracte la courbe en forme de sigmoïde. La fonction donne bien une probabilité (entre 0 et 1). Plus on s'éloigne de $\mu$, plus on est sûr de la prédiction (soit 0 vers $-\infty$, soit 1 vers $+\infty$).

Pour la régression logistique, on réécrit le terme dans l'exponentielle sous une forme linéaire
\begin{align}
p(x)=\frac{1}{1+e^{-(\beta_0 + \beta_1x)}}, \qquad\text{avec l'intercept $\beta_0=-\mu/s$ et le taux $\beta_1=1/s$.}
\end{align}
### Ajustement d'un modèle logistique pour une décision 0 ou 1
Comme en régression linéaire, on cherche à ajuster un modèle à des données. Cette fois-ci on mesure l'erreur d'ajustement avec la **fonction objectif logistique** (*logistic loss function*), qui est le négatif du logarithme de la vraisemblance. Pour commencer, on suppose que les données $X_k=(x_k,y_k)$ sont des points du plan, et on essaie d'ajuster une courbe logit à ces données. Pour une décision 0 ou 1, la valeur de la donnée $y_k$ est 0 ou 1.
Soit $p_k=p(X_k|\beta)$ la probabilité d'avoir l'issue 1 pour la donnée $X_k$. Essayons d'ajuster un modèle logit paramétré par $\beta=(\beta_0,\beta_1)$. Pour la régression linéaire, l'erreur d'ajustement serait le carré de la différence entre données $y_k$ et modèle.
Ici, on veut pénaliser la **surprise d'observer un résultat faux**. Donc si $p_k$ est proche de 0 alors que la donnée vaut 1, c'est une grosse surprise qui doit être pénalisé. La fonction $-\ln p_k$ convient car elle tend vers $+\infty$ pour $p_k$ proche de 0, et tend vers 0 pour $p_k$ proche de 1 (la prédiction est bonne). Inversement $-\ln (1-p_k)$ pénalise une donnée 0 alors que la prédiction est proche de 1.
Pour résumer, la fonction objectif logistique pour la donnée $x_k$ est :
\begin{align}
\ell_k(\beta)=\left\{ \begin{array}{l} -\ln(p_k) \quad \text{si $y_k$ vaut 1}\\ -\ln(1-p_k) \quad \text{sinon.}\end{array}\right. \quad \Leftrightarrow \quad \ell_k(\beta)=-y_k \ln(p_k) -(1-y_k)\ln(1-p_k).
\end{align}
L'expression à droite s'appelle aussi **entropie croisée** entre les distributions $y$ et $p$. C'est une sorte de distance entre distributions.
On cherche donc à minimiser les fonctions objectif de toutes les données, donc leur somme (ou de manière équivalente, leur moyenne, ce que l'on peut appeler aussi **coût empirique**):
\begin{align}
\tag{11}
\ell(\beta) =\sum_{k=1}^n \ell_k(\beta) = -\sum_{k=1}^n y_k \ln(p_k) +(1-y_k)\ln(1-p_k)
\end{align}
On vérifie que $\frac{d \ln(p_k)}{d \beta_0} =\frac{e^{-(\beta_0 + \beta_1 x_k)}}{1+e^{-(\beta_0 + \beta_1 x_k)}}=1-p_k$ et similairement $\frac{d \ln(1-p_k)}{d \beta_0}=-p_k$. Après quelques calculs, on trouve
\begin{align}
\frac{d\ell}{d\beta_0}=\sum_k (y_k - p_k) \qquad \text{et} \quad \frac{d\ell}{d\beta_1}=\sum_k (y_k - p_k)x_k.
\end{align}
On cherche alors **numériquement** pour quelles valeurs de $\beta_0$ et $\beta_1$ ces deux quantités s'annulent (les $p_k=1/(1+\exp(-\beta_0-\beta_1 x_k))$ cachent des non-linéarités qui rendent le problème non soluble analytiquement).
==Exemple==
On cherche dans quelle mesure le temps de révision (en heures) d'un étudiant l'aide à passer un examen (1: réussi, 0: raté). Sur une promotion, voilà les données collectées:
| heures $(x_k)$ | 0.50 | 0.75 | 1.0 | 1.25 | 1.50 | 1.75 | 1.75 | 2.0 | 2.25 | 2.5 |
| -------- | ---- | ---- | --- | ---- | ---- | ---- | ---- | --- | ---- | ----|
| réussite$(y_k)$| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| heures $(x_k)$ | 2.75 | 3.0 | 3.25 | 3.5 | 4.0 | 4.25 | 4.5 | 4.75 | 5.0 | 5.75 |
| -------- | ---- | --- | ---- | --- | --- | ---- | --- | ---- | --- | ---- |
| réussite$(y_k)$ | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
On peut donc former les deux fonctions $f(\beta_0,\beta_1)=\frac{d\ell}{d\beta_0}$ et $g(\beta_0,\beta_1)=\frac{d\ell}{d\beta_1}$ suivantes :
```python
# sagemath
var('x','b0','b1')
p(x)=1/(e^(-b1*x - b0) + 1)
f(b0,b1)=0-p(0.5)+0-p(0.75)+0-p(1)+0-p(1.25)+0-p(1.5)+1-2*p(1.75)+0-p(2.)+1-p(2.25)+0-p(2.5)+1-p(2.75)+0-p(3.)+1-p(3.25)+0-p(3.5)+1-p(4.)+1-p(4.25)+1-p(4.5)+1-p(4.75)+1-p(5.)+1-p(5.5)
g(b0,b1)=(0-p(0.5))*0.5+(0-p(0.75))*0.75+(0-p(1))*1.+(0-p(1.25))*1.25+(0-p(1.5))*1.5+(1-2*p(1.75))*1.75+(0-p(2.))*2.+(1-p(2.25))*2.25+(0-p(2.5))*2.5+(1-p(2.75))*2.75+(0-p(3.))*3.+(1-p(3.25))*3.25+(0-p(3.5))*3.5+(1-p(4.))*4.+(1-p(4.25))*4.25+(1-p(4.5))*4.5+(1-p(4.75))*4.75+(1-p(5.))*5.+(1-p(5.5))*5.5
C1=contour_plot( f(b0,b1), (b0,-6,0), (b1,0,3), cmap='hot',colorbar=true)+contour_plot( f(b0,b1), (b0,-6,0), (b1,0,3), fill=false, contours=(0.0,))
C2=contour_plot( g(b0,b1), (b0,-6,0), (b1,0,3), cmap='hot',colorbar=true)+contour_plot( g(b0,b1), (b0,-6,0), (b1,0,3), fill=false, contours=(0.0,))
(C1+C2).show()
```
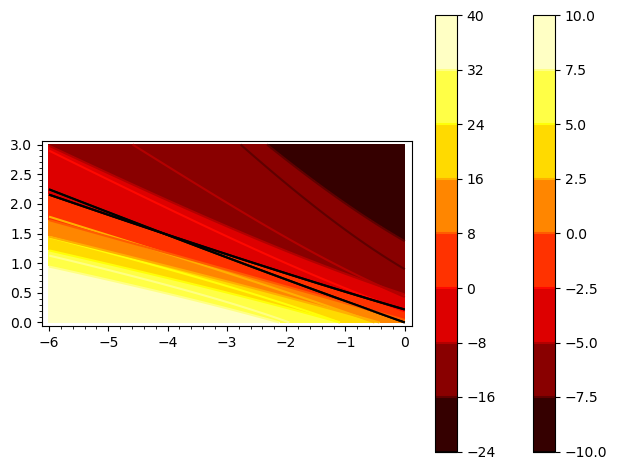
On voit que les 2 fonctions s'annulent à peu près pour $\beta_0 \approx -4.1$ et $\beta_1 \approx 1.5$.
:::info
Il ne vous a pas échappé que (11) est finalement aussi un maximum de vraisemblance. Par rapport à l'exemple précédent sur les jets de pile ou face, simplement on cherche à ajuster un modèle à 2 paramètres $(\beta_0,\beta_1)$ plutôt qu'un seul paramètre $q$.
:::
### Modèle logistique multi-classes, softmax et couche de classification logistique
On cherche maintenant à ajuster un modèle à $n$ variables explicatives organisées en un vecteur $\mathbf{x}:=(1, x_1, \ldots, x_n)$, et à identifier la probabilité d'appartenance à $K$ classes. Chacune des classes $z_j$ est modélisée par un vecteur de $n+1$ coefficients de régression $\mathbf{w_j}:=(\beta^{(j)}_0,\beta^{(j)}_1, \ldots, \beta^{(j)}_K)$. Chaque $\beta^{(j)}_0$ jouera le rôle d'une constante (en étant multiplié par le biais de 1). La matrice $\mathbf{W}$ regroupant tous ces vecteurs est donc l'inconnu que l'on cherche à déterminer/apprendre.
On va procéder comme pour le cas à 2 classes, où on utilisait une sigmoïde pour transformer le modèle linéaire en probabilité. Là, les modèles linéaires sont les produits scalaires $\mathbf{w_j} \cdot \mathbf{x}$, et l'extension de la sigmoïde à $k$-classes est la fonction **softmax**, définie ainsi
:::info
La fonction **softmax** (normalisée) ${\displaystyle \sigma :\mathbb {R} ^{K}\mapsto (0,1)^{K}}$, avec $K\geq 1$, est
\begin{align}
{\displaystyle \sigma (\mathbf {z} )_{i}={\frac {e^{z_{i}}}{\sum _{j=1}^{K}e^{z_{j}}}}\ \ {\text{ pour }}i=1,\dotsc ,K{\text{ et }}\mathbf {z} =(z_{1},\dotsc ,z_{K})\in \mathbb {R} ^{K}.}
\end{align}
Il est facile de voir que tous les $\sigma (\mathbf {z} )_{i}$ sont entre 0 et 1, et que leur somme fait 1. Toute translation des valeurs donne le même résultat. En général on fixe arbitrairement une classe à un résultat 1 (e.g. $z_K=1$).
:::
Intuitivement, l'exponentielle fait grandir la plus grande valeur beaucoup plus fort que les valeurs moindres. Donc la plus grande valeur à une probabilité plus proche de 1 que toutes les autres, qui du coup ont des probabilités plus faibles.
D'un point de vue calcul, cela peut se modéliser en une couche d'un réseau, avec une partie linéaire $\mathbf{W} \mathbf{x}$ et une fonction d'activation *softmax*.
| | Couche de classification logistique |
| -------- | -------- |
| $(x_1,\ldots,x_n)$ forme un **feature vector**, censé discriminé entre les différentes classes possibles. |  |
:::warning
La fonction **softmax** devrait plutôt être appelée **softargmax**, car c'est une approximation lisse de la fonction **argmax$(z_1,\ldots,z_k)$**, qui retourne un vecteur de 0, sauf un 1 là où est l'indice de la valeur maximum.
:::
La fonction objectif (ou **loss function**) pour une donnée $\mathbf{x_i}$ dont l'issue est la classe $y_i$, $1 \le y_i \le K$ est alors définie comme ci-dessus par $- \ln P( (y_i,\mathbf{x_i}) | \mathbf{W})$, où $P( (y_i,\mathbf{x_i} | \mathbf{W})$ est la **vraisemblance** de la donnée $(y_i,\mathbf{x_i})$ par rapport au modèle $\mathbf{W}$.
\begin{align}
\ell_i & = - \ln P( (y_i,\mathbf{x_i}) | \mathbf{W}) = -\ln \sigma( \mathbf{w_{y_i}} \cdot \mathbf{x_i})_{y_i} = -\ln \frac{e^{\mathbf{w_{y_i}}\cdot \mathbf{x_i}}}{\sum_k e^{\mathbf{w_k}\cdot \mathbf{x_i}}} \\
&= - \mathbf{w_{y_i}}\cdot \mathbf{x_i} + \ln \sum_k e^{\mathbf{w_k}\cdot \mathbf{x_i}} \\
\text{ou encore} \quad \ell_i & = - \mathbf{z_{y_i}} + \ln \sum_k e^{\mathbf{z_k}}
\end{align}
Si on cherche à minimiser la fonction objectif, on veut calculer le gradient de $\ell_i$ par rapport aux variables $\mathbf{W}$. On montre
\begin{align}
\frac{\partial{\ell_i}}{\mathbf{w_r}} = \left\{ \begin{array}{ll}-\mathbf{x_i}(1-P( (r,\mathbf{x_i}) | \mathbf{W})) \quad & \text{si $r=y_i$} \\ \mathbf{x_i}P( (r,\mathbf{x_i}) | \mathbf{W})) \quad & \text{si $r\neq y_i$} \end{array} \right.
\end{align}
Intuitivement, si on veut baisser $\ell_i$, on s'oppose au gradient. Si $r$ est la classe visée, alors il faut déplacer/aligner $\mathbf{w_r}$ dans la direction de la donnée, mais de moins en moins fort si la probabilité est déjà forte. Si $r$ n'est pas la classe visée, alors il faut déplacer/aligner $\mathbf{w_r}$ dans la direction opposée, et plus fortement si le réseau se trompait dans sa prédiction.
:::warning
Le calcul de $\frac{\partial{\ell_i}}{\mathbf{w_r}}$ s'établit en utilisant la "chain-rule".
:::
:::success
La **minimisation de la fonction objectif** ci-dessus par le **perceptron linéaire/softmax** est donc un calcul de **maximum de vraisemblance** d'appartenance à chaque classe.
:::
## Classification bayésienne
On rappelle que le maximum a posteriori (pour un modèle de paramètres $\theta$ et d'hyper-paramètres $\alpha$ sur des données $x_i$) pouvait s'obtenir en minimisant
\begin{align}
\tag{12}
\ell_{MAP}(\theta) := - \left[ \left( \sum_{i} \ln P( x_i | \theta,\alpha ) \right) + \ln p(\theta|\alpha) \right]
\end{align}
Avec les notations utilisées pour la régression multi-classes, nous avons les coefficients de régression $\mathbf{W}=\theta$ et les données étiquetées $(y_i,\mathbf{x_i})=x_i$. On voit que le MAP intègre en général plusieurs données, ce qui correspond à la pratique fréquente dans les réseaux de neurones de prendre les données par batch et de minimiser leur risque empirique. On réécrit (12) avec ces notations :
\begin{align}
\tag{13}
\ell_{MAP}(\mathbf{W}) := \left[ \left( \sum_{i} \underbrace{-\ln p( (y_i, \mathbf{x_i}) | \mathbf{W},\alpha )}_{\ell_i} \right) - \ln p(\mathbf{W}|\alpha) \right]
\end{align}
:::info
On voit que la **fonction objectif** pour trouver le **maximum a posteriori** est la même que celle du **perceptron linéaire/softmax** sommée/moyennée pour plusieurs données. La seule différence est dans le deuxième terme, qui tient compte d'un **probabilité a priori** sur le modèle, c'est-à-dire sur la distribution possibles des coefficients $\mathbf{W}$.
:::
:::warning
Si on reste sur la minimisation directe des $\ell_i$ alors tous les coefficients dans $\mathbf{W}$ sont équiprobables. Cela veut dire que certains coefficients peuvent exploser vers l'infini.
:::
On suppose donc en général que les coefficients de $\mathbf{W}$ sont plus probablement proches de 0 que de l'infini. On peut par exemple supposer que chaque coefficient $w_{i,j}$ suit une loi normale centrée en 0 de variance $\lambda^2$. On note que **$\lambda$ est un hyper-paramètre**. Si on suppose que les coefficients sont des variables aléatoires indépendantes, on a
\begin{align}
-\ln p(\mathbf{W}|\alpha) & = - \ln \prod_{i,j} p( w_{i,j} | \lambda) && \text{(car les coefficients sont indépendants)}\\
& = - \sum_{i,j} \ln p( w_{i,j} | \lambda) && \text{(car le log transforme $\times$ en $+$)} \\
& = -\sum_{i,j} \ln \frac{1}{\sqrt{2\pi}\lambda}e^{-\frac{w_{i,j}^2}{2\lambda^2}} && \text{(car c'est une loi normale centrée en 0)}\\
& = \underbrace{K(n+1)\ln (\sqrt{2\pi}\lambda)}_\text{constante} + \frac{1}{2\lambda^2} \sum_{i,j} {w_{i,j}^2} && \text{(car $\ln (\gamma e^x) = (\ln \gamma) + x$)}\\
\end{align}
Si on cherche le minimum de cette fonction, la constante est inutile. Le terme de droite est proportionnel à n'importe quel norme sur la matrice $\mathbf{W}$. Pour résumer, on a :
\begin{align}
\ell_{MAP}(\mathbf{W}) = \sum_i \ell_i + \frac{1}{2\lambda^2} \| \mathbf{W} \|_2^2
\end{align}
On trouve alors facilement
\begin{align}
\frac{\partial \ell_{MAP}}{\mathbf{w_r}} = \underbrace{\sum_i \frac{\partial{\ell_i}}{\mathbf{w_r}}}_\text{perceptron linéaire/softmax} + \underbrace{\frac{1}{\lambda^2} \mathbf{W}}_\text{régularisation}
\end{align}
:::info
Si $\eta$ est le taux d'apprentissage, alors, pour un batch de données $(y_i,\mathbf{x_i})$, on met à jour les coefficients $\mathbf{W}^{(k)}$ au temps $k$ en allant dans la direction opposée du gradient ainsi
\begin{align}
\mathbf{W}^{(k+1)}= \left(1- \eta \frac{1}{\lambda^2}\right) \mathbf{W}^{(k)}- \eta \left\{ \begin{array}{ll}-\mathbf{x_i}(1-P( (r,\mathbf{x_i}) | \mathbf{W}^{(k)})) \quad & \text{si $r=y_i$} \\ \mathbf{x_i}P( (r,\mathbf{x_i}) | \mathbf{W}^{(k)}) \quad & \text{si $r\neq y_i$} \end{array} \right.
\end{align}
avec $P( (y_i,\mathbf{x_i}) | \mathbf{W}) = \mathrm{softmax}( \mathbf{w_{y_i}} \cdot \mathbf{x_i})_{y_i}$.
:::
# Ressources
- [Inférence bayésienne (Wikipedia)](https://fr.wikipedia.org/wiki/Inférence_bayésienne)
- [Maximum de vraisemblance (wikipedia)](https://fr.wikipedia.org/wiki/Maximum_de_vraisemblance)
- [Logistic regression (Wikipedia)](https://en.wikipedia.org/wiki/Logistic_regression)
- [German tank problem](https://en.wikipedia.org/wiki/German_tank_problem)
- [vidéo du cours S. Mallat, collège de France](https://www.college-de-france.fr/fr/agenda/cours/apprentissage-par-reseaux-de-neurones-profonds/optimisation-un-reseau-par-maximum-de-vraisemblance#:~:text=L%27optimisation%20d%27un%20réseau,le%20risque%20doit%20être%20différentiable.)