---
title: INFO911 (TP1) Espaces colorimétriques, Egalisation d'histogramme, et tramage de Floyd-Steinberg
---
INFO911 (TP1) Espaces colorimétriques, Egalisation d'histogramme, et tramage de Floyd-Steinberg
===
[TOC]
> [name=Jacques-Olivier Lachaud][time=Novembre 2020][time=September 2025][color=#907bf7]
###### tags: `info911` `tp`
Retour à [INFO911 (Main) Traitement et analyse d'image](https://codimd.math.cnrs.fr/s/UE_B59gMy)
Ce TP étudie principalement sur l'espace des valeurs d'une image, et vous propose de travailler sur la dynamique des images noir et blanc et couleur, sur l'utilisation de l'espace colorimétrique HSV, et sur la quantification des valeurs par tramage.
> Certains reconnaitront une partie du tp C++ de l'an dernier.
## 1. Correction de la dynamique par égalisation d'histogramme
### a. Programme initial
Vous pouvez partir de ce bout de code qui charge une image et l'affiche:
```cpp=
#include <iostream>
#include <opencv2/highgui.hpp>
#include <opencv2/imgproc.hpp>
using namespace cv;
int main()
{
int old_value = 0;
int value = 128;
namedWindow( "TP1"); // crée une fenêtre
createTrackbar( "track", "TP1", &value, 255, NULL); // un slider
Mat f = imread("lena.png"); // lit l'image "lena.png"
imshow( "TP1", f ); // l'affiche dans la fenêtre
while ( waitKey(50) < 0 ) // attend une touche
{ // Affiche la valeur du slider
if ( value != old_value )
{
old_value = value;
std::cout << "value=" << value << std::endl;
}
}
}
```
Notez déjà comment on rajoute un `slider` à la fenêtre principale, et comment on récupère sa valeur. La fonction `waitKey()` gère tous les événements associés à la fenpêtre. Il faut donc l'appeler régulièrement. Ici le `50` correspond à 50ms d'attente. La fonction elle-même renvoie un nombre négatif si rien ne s'est passé, et sinon la partie de poids faible de l'entier retourné est le code ASCII de la touche pressée.
Modifiez le code initial pour que l'utilisateur puisse donner le nom de l'image à charger comme premier paramètre au programme. Si aucun nom n'est donné, le programme doit afficher le "Usage" habituel:
```
Usage: ./prog <nom-fichier-image>
```
:::warning
OpenCV recommande de créer les Trackbars ainsi, et de récupérer leur valeur par des getTrackbarPos:
```c++
createTrackbar( "track", "TP1", nullptr, 255, nullptr); // un slider
setTrackbarPos( "track", "TP1", value );
...
int new_value = getTrackbarPos( "track", "TP1" );
```
Malheureusement cela provoque un `segmentation fault` sur mon MacOS (OpenCV4.6). La façon de faire ci-dessus fait un warning mais fonctionne sans problème.
:::
### b. Conversion en niveaux de gris
Dans un premier temps, on va traiter des images en niveaux de gris. Rajoutez dans le code ce qu'il faut pour tester si l'image en entrée est déjà en niveaux de gris (voir `cv::Mat::type()` ou `cv::Mat::channels()`) et sinon convertit l'image en niveaux de gris.
> Vous pouvez le faire a la mano par parcours de l'image, ou utiliser `cv::cvtColor`. [color=#907bf7]
> Le descriptif de [conversion de couleur](https://docs.opencv.org/master/de/d25/imgproc_color_conversions.html) de cette fonction peut être utile.
L'image affichée doit donc être en niveaux de gris maintenant.
|  |  |
| ------------------------------------------------------------------------------------ | ------------------------------------------------------------------------------------ |
### c. Calcul de l'histogramme et de l'histogramme cumulé
On rappelle que l'==histogramme $h_I$== mesure la proportion de pixels de $I$ qui ont une même valeur ($\#$ désigne le nombre d'éléments ou cardinal d'un ensemble):
$$
\forall v \in V, h_I[v] = \frac{\# \{ p \in R, I[p] = v \}}{\#\{R\}}.
$$
Ici $V$ sont les entiers de 0 à 255, et $R$ est le domaine de l'image $I$, un rectangle.
L'==histogramme cumulé $H_I$== cumule les valeurs de $h_I$:
$$
\forall v \in V, H_I[v] = \sum_{ i \in V, i \le v} h_I[v].
$$
Comme on a normalisé par le nombre total de pixels, $h_I[v]$ est la probabilité qu'un pixel de $I$ ait la valeur $v$, et $H_I[v]$ est la probabilité qu'un pixel de $I$ ait une valeur $\le v$.
Ecrivez deux fonctions pour calculer ces histogrammes:
```cpp=
std::vector<double> histogramme( Mat image );
std::vector<double> histogramme_cumule( const std::vector<double>& h_I );
```
Puis afficher l'histogramme de l'image donnée en entrée dans une autre fenêtre (utilisez `nameWindow`).

On créera une image 512x256 dans lequel on affichera les histogrammes (faire les tracés avec de simples boucles). Notez que pour l'histogramme $h_I$, on calcule la valeur maximale pour le remettre à l'échelle à l'affichage et qu'il soit plus visible.
```cpp=
cv::Mat afficheHistogrammes( const std::vector<double>& h_I,
const std::vector<double>& H_I )
{
cv::Mat image( 256, 512, CV_8UC1 );
...
}
```
> Il existe une fonction de calcul des histogrammes dans OpenCV, [cv::calcHist](https://docs.opencv.org/3.4/d6/dc7/group__imgproc__hist.html#ga4b2b5fd75503ff9e6844cc4dcdaed35d). Elle est très générique, donc pas si facile que ça à utiliser. [color=#907bf7]
### d. Egalisation de l'image
On va maintenant corriger la dynamique de l'image en utilisant la méthode de l'égalisation d'histogramme.
On cherche une transformation $f: V \rightarrow V$ tel que $J = f \circ I$, pixels $p \in R$
$$
\frac{v}{255} = H_{f \circ I}[v] = \frac{\#\{p \in R, f \circ I[p] \le v \}}{\#\{p \in R\}} = \frac{\#\{p \in R, I[p] \le f^{-1}[v] \}}{\#\{p\in R\}} = H_{I}[ f^{-1}[v]]
$$
Soit $w=f^{-1}[v]$, on a $v=f[w]$, il vient $\frac{f[w]}{255}=H_I[w]$, i.e. $f[w] = 255 \cdot H_I[w]$
On applique $f$ sur tous les pixels de $I$ pour obtenir $J$.
Ecrivez la fonction d'égalisation. Affichez l'image égalisée et les histogrammes égalisés.
|  |  |  |
| --- | ------------------------------------------------------------------------------------------------------- | ------------------------------------------------------------------------------------------------ |
| Image $I$ | Image égalisée $J = f \circ I$ | Histogrammes égalisées $h_J$ et $H_J$ |
### e. Gestion des images couleur
On va gérer les images couleurs en ne calculant l'image égalisée que sur la luminosité des pixels. On va donc traiter les images couleurs en convertissant l'image (codée BGR) en une image codée HSV.
Ensuite, on ne calculera l'histogramme que sur le canal V de HSV, puis on égalisera ce canal. Ensuite on reconvertit l'image obtenue en BGR pour l'afficher.
> La fonction `cv::cvtColor` peut être utilisée pour faire cette conversion. Ensuite vous disposez des fonctions `cv::split` et `cv::merge` pour séparer les canaux ou les fusionner. [color=#907bf7]
|  |  |
| -------- | -------- |
| 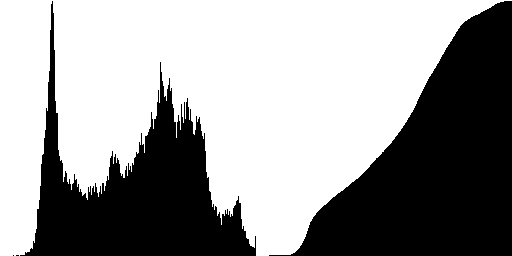 | 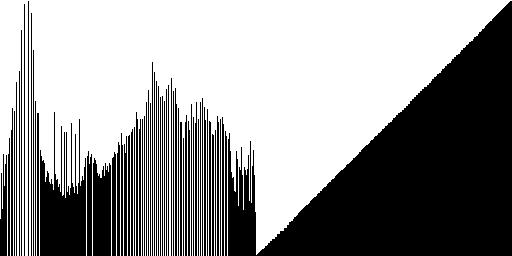 |
:::warning
Il faut bien utiliser `std::vector<Mat> HSV` et non `Mat HSV[3]` pour que `cv::merge` fonctionne.
:::
> On peut aussi utiliser l'espace TLS (HLS en anglais) et utiliser le channel L. Les résultats ont tendance à être un peu moins bons dans la plupart des cas. [color=#907bf7]
## 2. Tramage des images
### a. Introduction au tramage
Vous allez faire un autre programme dont l'objectif va être de réaliser un tramage de l'image. Dit autrement, il s'agit de requantifier l'image en niveaux de gris ou couleur dans un espace de valeurs (beaucoup) plus petit.
En anglais, on parle de *dithering* ou *half-toning*.
Historiquement, le tramage était utilisé pour transmettre une image sur un média avec très peu de couleurs:
* imprimante noir & blanc: on ne pouvait que tracer ou pas un pixel
* fax: pareil, on ne pouvait transmettre que des pixels noir et blanc
* impression couleur CMYK: on ne peut tracer que des pixels cyan, magenta, yellow, black
* écran: les premiers ordinateurs avaient des palettes de couleurs assez faible, on dessinait ou prenait des photos en couleurs puis on les tramait pour que l'ordinateur cible puisse afficher une image proche.
* ZX80: 2 couleurs (noir et blanc)
* apple II: 8 couleurs
* spectrum: 8 couleurs (résolution pixel 256x192, résolution couleur 32x24)
* commodore 64: 16 couleurs (même résolution pixel et couleur 320x200)
* atari ST: 16 couleurs parmi 512 possibles (320x200)
* conversion en formats limités: GIF a par exemple 256 couleurs max.
* transfert vers une palette de couleur donnée
Aujourd'hui, le tramage reste utilisé pour faire de l'impression, mais aussi exploité pour faire des effets artistiques, ou une variante du tramage peut être utilisé pour imprimer de grandes affiches (de près, on voit bien les 4 pigments CMYK).
Il existe de nombreux algorithmes de tramages, les plus basiques étant basés sur l'aléatoire ou regroupant des blocs de pixels, les plus évolués introduisant des sortes de pinceaux stylisés qu'ils superposent (e.g., voir cet [article](https://infoscience.epfl.ch/record/99842/files/maad.pdf)).

### b. Tramage par algorithme de Floyd-Steinberg
C'est un grand classique des algorithmes de tramage, car il est rapide, simple à calculer, et donne des résultats très sympas. Son principe est très simple. Pour chaque pixel, on quantifie sa valeur. Si on est dans le cas binaire, on choisit le noir ou le blanc. On fait donc une erreur $e$ entre la valeur du pixel et la valeur quantifiée. On écrit la valeur quantifiée dans le pixel et on **propage** l'erreur à ses 4 voisins plus loin sur le scanline.
| ----> | ----> | ----> |
|:----------------:|:-----------------------:|:----------------:|
| ----> | pixel $e=v-\widehat{v}$ | $+\frac{7}{16}e$ |
| $+\frac{3}{16}e$ | $+\frac{5}{16}e$ | $+\frac{1}{16}e$ |
Pour plus de détails voir l'[Algorithme de Floyd-Steinberg](https://fr.wikipedia.org/wiki/Algorithme_de_Floyd-Steinberg) sur Wikipedia.
|  |  |
|:----:|:----:|
| lena 256x256 (niveaux de gris) | lena 256x256 tramé par Floyd-Steinberg |
Vous ferez une fonction qui réalise ce tramage. Elle prend en entrée une image `CV_8UC1` et sort une image de même taille et du même type.
```cpp=
cv::Mat tramage_floyd_steinberg( cv::Mat input );
```
:::info
Dans cette fonction, le plus simple est de passer par une image de nombre réels, par exemple `CV_32FC1` pour faire les calculs et propager l'erreur.
:::
:::info
Ici, il faudra utiliser les fonctions `image.at<float>(x, y)` pour aller chercher les valeurs des pixels voisins, ou les modifier.
:::
### c. Tramage RGB par algorithme de Floyd-Steinberg
Il est très facile maintenant de tramer des images couleurs, simplement en tramant chacun des canaux séparément. Adaptez votre programme pour qu'il traite indifférement des images en niveaux de gris ou couleur.
|  |  |
|:----:|:----:|
| lena 256x256 (couleur) | lena 256x256 tramé par Floyd-Steinberg |
Ce tramage crée des pixels de 8 couleurs différentes: noir, rouge, vert, bleu, cyan, magenta, jaune, et noir.
### d. Tramage générique, application à l'impression CMYK
Le tramage précédent n'est pas adapté à l'impression, qui ne dispose que de 4 couleurs d'encre (cyan, magenta, yellow, noir), plus le blanc du papier.
Pour pouvoir réaliser un tramage adapté à l'impression, nous devons adapter différemment notre algorithme de Floyd-Steinberg. L'idée principale est de travailler avec une erreur de diffusion **vectorielle** (i.e. 3 valeurs d'erreur: 1 sur rouge, 1 sur vert, 1 sur bleu).
L'algorithme prend en entrée une image BGR, et un vecteur de couleurs, en sortie une image BGR.
```cpp=
cv::Mat tramage_floyd_steinberg( cv::Mat input,
std::vector< cv::Vec3f > colors )
```
Dans le cas du tramage CMYK, `colors` contiendra les cinq couleurs possibles, codées en 3 flottants 32 bits chacune. Par exemple cyan = `cv::Vec3f( {1.0, 1.0, 0.0})`.
On écrit une fonction qui calcule la distance entre deux couleurs `cv::Vec3f`, une autre qui retourne la couleur la plus proche d'une couleur donnée, parmi le vecteur de couleurs donné, et enfin une dernière qui calcule le vecteur erreur entre 2 couleurs (leur différence).
```cpp=
float distance_color_l2( cv::Vec3f bgr1, cv::Vec3f bgr2 );
int best_color( cv::Vec3f bgr, std::vector< cv::Vec3f > colors );
cv::Vec3f error_color( cv::Vec3f bgr1, cv::Vec3f bgr2 );
```
> On choisira ici la simple distance Euclidienne entre 2 couleurs, i.e. la racine carrée du carré des différences entre chaque composante de couleur. Evidemment une distance dans un espace de couleur serait peut-être plus intéressante ici. [color=#907bf7]
L'algorithme suit alors le principe de l'algorithme précédent:
```cpp=
cv::Mat tramage_floyd_steinberg( cv::Mat input,
std::vector< cv::Vec3f > colors )
{
// Conversion de input en une matrice de 3 canaux flottants
cv::Mat fs;
input.convertTo( fs, CV_32FC3, 1/255.0);
// Algorithme Floyd-Steinberg
Pour chaque pixel (x,y) Faire
{
c <- fs.couleur(x,y)
i <- best_color( c, colors )
e <- error_color( c, colors[ i ] );
fs.couleur(x,y) <- colors[ i ]
On propage e aux pixels voisins
}
// On reconvertit la matrice de 3 canaux flottants en BGR
cv::Mat output;
fs.convertTo( output, CV_8UC3, 255.0 );
return output;
}
```
Voilà les résultats que vous pouvez obtenir pour CMYK.
| Input | Tramage RGB | Tramage CMYK |
|:----------------------------------------------------------------------------------------------:|:---------------------------------------------------------------------------------------------------:|:----------------------------------------------------------------------------------------------------:|
|  |  | 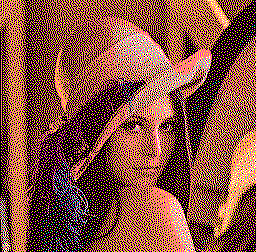 |
|  |  | 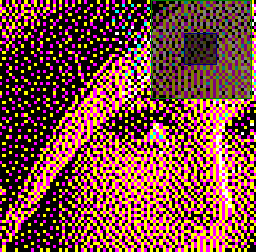 |
> Cet algorithme est très générique, car vous pouvez cibler maintenant n'importe quel choix de couleurs données. [color=#907bf7]
## 3. Intégration dans un flux vidéo
Il est très simple de capturer un flux vidéo en OpenCV, et de faire un traitement sur les images successives en temps réel (pour des traitements simples). On va faire une application qui permet à l'utilisateur d'égaliser ou non en temps réel le flux vidéo, et de le tramer ou non en temps réel.
### a. Capture du flux vidéo
Voilà un code minimal de capture vidéo, qui transforme en niveaux de gris avant affichage. On voit comment tester la touche `'q'` pour quitter.
```cpp=
#include "opencv2/imgproc.hpp"
#include "opencv2/highgui.hpp"
using namespace cv;
int main(int, char**)
{
VideoCapture cap(0);
if(!cap.isOpened()) return -1;
Mat frame, edges;
namedWindow("video", WINDOW_NORMAL);
for(;;)
{
cap >> frame;
cvtColor(frame, edges, COLOR_BGR2GRAY);
imshow("video", edges);
int key_code = waitKey(50); // 50 ms entre les frames
int ascii_code = key_code & 0xff;
if( ascii_code == 'q') break;
}
return 0;
}
```
### b. Ajout de l'égalisation et du tramage
Intégrez vos fonctions développées précédemment dans ce programme.
Ensuite créer des variables booléennes pour forcer ou non un traitemement couleur ou niveaux de gris, pour faire ou pas l'égalisation, pour faire ou non le tramage.
## 4. Evaluation
A la fin de la séance, chaque groupe doit me montrer où il en est et ses réalisations fonctionnelles.