# Algo Prog 2021-2022: TP2 ###### tags: `algo` `bourg` `c++` `iut` `tp` ## Exercice 1: Jeu du pendu Dans cet exercice, on vous propose de coder le jeu du pendu. Demandez à votre enseignant de vous faire un rappel des règles au tableau si vous ne le connaissez pas. Dans un premier temps, le mot à trouver sera codé en dur dans votre appli. Par la suite, il sera choisi au hasard par votre programme dans le dictionnaire (qui vous sera fourni sous forme de fichier). ### Constantes et variables globales Dans votre programme, vous allez devoir travailler avec deux mots récurrents: celui à trouver (``mot_a_trouver``, de type ``char[]``), et celui que le joueur construit (``mot_courant``, de type ``char[]``). Au départ ce dernier ne contient donc que des lettres inconnues. Pour des raisons de commodité, nous déclarerons ces deux chaines de caractères comme des variables globales dont la taille ne dépassera pas une certaine constante (``TAILLE``, que vous initialiserez à 25). Vous déclarerez également une constante ``NB_COUPS_MAX`` correspondant au nombre d'erreurs maximum avant d'être pendu. Initialisez-là à 7. :::spoiler ````C++ const int TAILLE = 25; const int NB_COUPS_MAX = 7; char mot_courant[TAILLE]; char mot_a_trouver[TAILLE]; ```` ::: ### Initialisations Avant de commencer la partie, nous avons besoin d'initialiser les deux mots définis précédemment: - Dans votre main, initialisez le mot à trouver avec le mot de votre choix (on verra par la suite comment choisir un mot au hasard dans le dictionnaire). :::info N'oubliez pas l'utilisation de ``strcpy_s`` ::: :::spoiler ````C++ int main(){ strcpy_s(mot_a_trouver,"bonjour"); } ```` ::: - Pour le mot courant (celui du joueur), il est au départ initialisé avec des lettres inconnues, et sa taille est identique à celle du mot à trouver. On choisira le caractère '_' (underscore) pour les lettres inconnues. Faites une fonction qui permet d'initialiser le mot courant comme une chaine respectant ces critères. Appelez ensuite cette fonction dans votre programme principal. :::spoiler ````C++ void init_mot_courant() { int i = 0; while (mot_a_trouver[i] != '\0') { mot_courant[i] = '_'; i++; } mot_courant[i] = '\0'; } ```` ::: ### Affichage d'un mot Codez une fonction qui prend une chaine de caractères en paramètre et qui affiche cette chaine avec un espace entre chaque caractère. Dans votre main, testez cette fonction sur le mot courant après l'avoir initialisé, vous devriez voir qqch du genre: ```` _ _ _ _ _ _ ```` :::spoiler ````C++ void affiche_mot(char ch[]) { int i = 0; while (ch[i] != '\0') { cout << ch[i] << ' '; //on sépare les lettres par des espaces i++; } } ```` ::: ### Jouer un coup Codez la fonction ``void jouer(char lettre, int& compteur)`` qui simule un coup du joueur qui propose la lettre passée en paramètre. Si cette lettre est présente dans le mot à trouver, toutes les occurrences de cette lettre remplacent les caractères inconnus correspondant dans le mot courant ; le compteur est inchangé. Si cette lettre n'est pas présente, le mot courant est inchangé et le paramètre compteur est décrémenté. :::spoiler ````C++ void jouer(char lettre, int& compteur) { int i = 0; bool present = false;//indique si la lettre est presente dans le mot a trouver while (mot_a_trouver[i] != '\0') { if (mot_a_trouver[i] == lettre) { present = true; //la lettre apparait au moins une fois mot_courant[i] = lettre; } i++; } if (present == false) // on perd une vie si on n'a pas trouvé la lettre compteur--; } ```` ::: ### Affichage du pendu Il n'est pas simple de dessiner un pendu à la console. On choisira plutot d'afficher le nombre d'erreurs restant autorisé sous forme d'étoiles (un peu comme des nombres de vies). Au départ, on aura donc une ligne de NB_COUPS_MAX étoiles. Faites une fonction d'affichage qui prend un entier $i$ en paramètre et affiche une ligne de $i$ étoiles. :::spoiler ````C++ void affiche_pendu(int compteur) { cout << "PENDU: "; for (int i = 1; i <= compteur; i++) cout << "*"; cout << endl; } ```` ::: ### Fin de partie Faites une fonction booléenne ``bool gagne()`` qui retourne vrai si et seulement si toutes les lettres du mot courant ne sont plus inconnues. :::spoiler ````C++ bool gagne() { int i = 0; while (mot_courant[i] != '\0' && mot_courant[i] != '_') i++; return mot_courant[i] == '\0'; } ```` ::: ### Programme principal En utilisant les fonctions décrites précédemment, complétez votre programme principal afin de faire une partie de pendu. 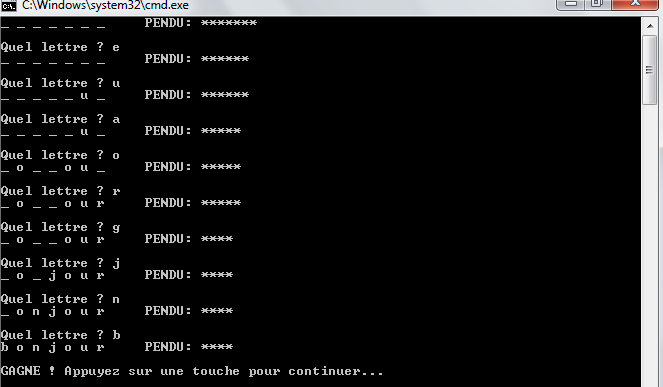Exemple d'affichage:  :::spoiler ````C++ void main() { char lettre; srand(time(NULL)); strcpy_s(mot_a_trouver,TAILLE, "bonjour"); init_mot_courant(); int compteur = NB_COUPS_MAX; affiche_mot(mot_courant); cout << " "; affiche_pendu(compteur); cout << endl; while (compteur>0 && gagne() == false) { cout << "Quelle lettre ? "; cin >> lettre; jouer(lettre, compteur); affiche_mot(mot_courant); cout << " "; affiche_pendu(compteur); cout << endl; } if (compteur == 0) { cout << "PERDU ! "; affiche_mot(mot_a_trouver); } else cout << "GAGNE ! "; } ```` ::: ### Tirage d'un mot aléatoire dans le dictionnaire Vous trouverez [ici](https://perso.liris.cnrs.fr/eric.duchene/algo/DicFra.csv) le fichier ``DicFra.csv`` qui contient la liste des mots du dictionnaire ainsi que leur définition. Ouvrez-le avec WordPad ou le bloc notes pour voir ce qu'il renferme. Dans ce fichier, nous ne nous intéresserons qu'à la liste des mots (entre guillemets au début de chaque ligne), et pas à leur définition. Il y a exactement 27 286 mots dans ce fichier. Faites une fonction init_alea qui choisit un nombre n au hasard entre 1 et 27 286, et initilialise le mot à trouver avec le nième mot du dictionnaire. Jouez en utilisant cette fonction maintenant. :::spoiler ````C++ void lire_mot_aleatoire() { ifstream entree("DicFra.csv", ios::in); char ligne[10000]; int alea = rand() % 27286; if (!entree) cout << "probleme ouverture fichier" << endl; else { for (int i = 1; i<alea; i++) { entree.getline(ligne, 10000); //on lit les lignes au fur et à mesure } int i; entree.getline(mot_a_trouver, 100, ',');//on lit le mot jusqu'à la virgule //il reste à enlever les guillemets int lg = strlen(mot_a_trouver); for (i = 0; i<lg - 2; i++) mot_a_trouver[i] = mot_a_trouver[i + 1]; mot_a_trouver[i] = '\0'; entree.close(); } } ::: ## Exercice 2: le voyageur de commerce Un voyageur de commerce doit visiter, pour son travail, N villes numérotées de 1 à N. Il doit ensuite retourner à son point de départ. Il connaît les distances entre les villes. Il part de la ville numérotée DepartVC et y revient. Il cherche un ordre de visite qui "minimise" la distance totale parcourue. Nous vous indiquons ici un algorithme qui conduit à une bonne solution du problème, mais pas à sa solution optimale. Cet algorithme utilise les deux principes suivants : - passer une et une seule fois dans chaque ville. - après avoir visité la ville numérotée DepartEtape, se rendre à la ville ArriveeEtape, non encore visitée, la plus proche de la ville DepartEtape. ### Variables globales et constantes du problème **N** nombre de villes à visiter. C'est une constante de votre problème, initialisez-là à 20. **Dist** tableau des distances entre les villes. Ici Dist est un tableau d'entiers, à deux dimensions, ``Dist[i][j]`` est la distance entre la ville i et la ville j. Le tableau Dist est donc un tableau carré $(N+1)\times (N+1)$, symétrique, et de diagonale principale nulle. Les cases d'indice 0 ne seront pas considérées (comme les indices des villes vont de 1 à N). **NomVilles** Tableau contenant le noms des villes: c'est donc un tableau de chaines de caractères de taille $(N+1)\times 30$ (on supposera que les villes n'ont pas plus de 30 caractères dans leur nom). **DepartVC** numéro de la ville de départ, on supposera que c'est la ville 1 pour commencer. ### Variables locales **DepartEtape** numéro de la dernière ville visitée **ArriveeEtape** numéro de la ville non visitée la plus proche de la ville DepartEtape, ce sera la ville étape suivante **DejaVisitee** tableau de booléens indiquant les villes déjà visitées : - DejaVisitee[i] = true si la ville numéro i est déjà visitée - DejaVisitee[i] = false si la ville numéro i n'est pas encore visitée **Etape** tableau de (N+1) entiers contenant la liste des villes visitées, dans l'ordre de la visite, c'est-à-dire : Etape[i] = la ième ville visitée. Pour simplifier on posera Etape[N+1] = Etape[1] = DepartVC. **LgCumulee** tableau d'entiers représentant la longueur cumulée du parcours effectué par le voyageur de commerce depuis la ville DepartVC jusqu'à chaque ville i ; LgCumulee[i] = longueur cumulée, dans l'itinéraire obtenu, entre la ville DepartVC et la ième ville visitée. On a donc LgCumulee[N+1] = longueur totale du parcours. ### Acquisition des données Les données vous sont fournies dans un fichier .txt [ici](https://perso.liris.cnrs.fr/eric.duchene/algo/villes.txt). Ouvrez-le pour voir à quoi il ressemble: vous verrez la liste des noms des villes et le tableau des distances (rempli à moitié, l'autre moitié est symétrique). Faites une fonction qui lit ce fichier et initialise les tableaux Dist et NomVilles. Testez-là dans votre main. ### Algorithme Implémentez maintenant l'algorithme proposé ci-dessous, en commençant par initialiser vos variables locales correctement. tant que Etape[i] n'est pas décidé pour tout i, faire (a) calculer ArriveeEtape, la ville non visitée la plus proche de DepartEtape (b) mettre à jour notamment DepartEtape, DejaVisitee, Etape, LgCumulee ### Affichage Affichez les résultats sous la forme suivante : ```` Etape Ville Longueur 1 ... ... ... ... ... N+1 ... ... ```` ### Amélioration En faisant varier DepartVC pour chacune des villes, proposer le meilleur tour possible.