--- title: Sur l'épreuve pratique NSI — sujet n°20, 2022 langs: fr-fr tags: c3i, ep ... # Sur l'épreuve pratique NSI — sujet n°20, 2022 > C3I : commission inter-IREM informatique > [univ-irem.fr/c3i](https://www.univ-irem.fr/spip.php?rubrique506) > [c3i-contact@groupes.renater.fr](mailto:c3i-contact@groupes.renater.fr) > 27 janvier 2023 - Thème de l'exercice 1 : L'opérateur « ou exclusif » entre deux tableaux de bits - Thème de l'exercice 2 : Carré magique ## Introduction Ce document propose une analyse des deux exercices du sujet n°20 de l'épreuve pratique de Numériques et sciences informatiques (NSI) du baccalauréat 2022. Nous proposons pour chaque exercice une transcription de l'énoncé, des solutions possibles, une analyse des notions en jeu et de leur présentation dans l'exercice, et des suggestions éventuelles d'énoncés alternatifs. ## Exercice 1 **Mots-clés :** ou exclusif, tableaux ### Énoncé :::info EXERCICE 1 (4 points) L'opérateur « ou exclusif » entre deux bits renvoie 0 si les deux bits sont égaux et 1 s'ils sont différents : 0 ⊕ 0 = 0 , 0 ⊕ 1 = 1 , 1 ⊕ 0 = 1 , 1 ⊕ 1 = 0 On représente ici une suite de bits par un tableau contenant des 0 et des 1. Exemples : ```python a = [1, 0, 1, 0, 1, 1, 0, 1] b = [0, 1, 1, 1, 0, 1, 0, 0] c = [1, 1, 0, 1] d = [0, 0, 1, 1] ``` Écrire la fonction `xor` qui prend en paramètres deux tableaux de même longueur et qui renvoie un tableau où l’élément situé à position `i` est le résultat, par l’opérateur « ou exclusif », des éléments à la position `i` des tableaux passés en paramètres. En considérant les quatre exemples ci-dessus, cette fonction doit passer les tests suivants : ```python assert(xor(a, b) == [1, 1, 0, 1, 1, 0, 0, 1]) assert(xor(c, d) == [1, 1, 1, 0]) ``` ::: ### Propositions de solutions Version avec les listes en compréhension et le modulo : ```python def xor(a, b): return [(a[i] + b[i]) % 2 for i in range(len(a))] ``` Versions à la main probablement attendues : ```python def xor(a, b): resultat = [] for i in range(len(a)): if a[i] == b[i]: resultat.append(0) else: resultat.append(1) return resultat ``` ```python def xor(a, b): resultat = [] for i in range(len(a)): resultat.append(a[i]^b[i]) return resultat ``` ```python def xor(a, b): longueur = len(a) resultat = [0]*longueur for i in range(longueur): resultat[i] = a[i]^b[i] return resultat ``` Versions en passant par les booléens : ```python def xor(a, b): return [int(a[i] != b[i]) for i in range(len(a))] ``` ```python import operator def xor(a, b): return [operator.xor(a[i], b[i]) for i in range(len(a))] ``` En contournant l'itération : ```python import operator def xor(a, b): return list(map(operator.xor, a, b)) ``` ### Analyse L'opérateur *ou exclusif* est à la fois un opérateur logique qui s'applique aux valeurs de vérité et un opérateur qui s'applique aux bits et aux chaînes de bits selon la convention décrite dans l'énoncé. À ce titre, il s'applique aussi aux entiers positifs en considérant leur écriture binaire. Python fournit l'opérateur binaire `^` (et la fonction `operator.xor`) pour représenter cette opération sur les booléens et les entiers. Par exemple : ```python >>> 5 ^ 6 3 >>> (2**100 + 1) ^ 2**100 1 ``` Dans le premier cas, le résultat est $3$ parce que $5$ et $6$ s'écrivent respectivement $(101)_2$ et $(110)_2$ en binaire. Le ou exclusif bit par bit donne donc $(011)_2$ qui est une écriture binaire de $3$. Voici un exemple qui rend ce fonctionnement plus explicite: ```python >>> 0b101 ^ 0b110 3 >>> bin(0b101 ^ 0b110) '0b11' ``` L'opérateur de comparaison `!=`, suggéré par la première phrase de l'énoncé, coïncide avec `^` lorsqu'il est appliqué aux valeurs booléennes, et uniquement dans ce cas. Pour représenter des chaînes de bits, on a habituellement recours à des entiers. Cet énoncé utilise des tableaux de bits. L'intention est donc bien de travailler la notion de tableau pour elle-même, avec les savoirs associés : parcours, accès à un élément par son indice, construction ou modification d'un tableau, etc. Par ailleurs, la référence à un indice `i` dans l'énoncé suggère l'usage de l'itération. Si l'on considère l'opération demandée sur les tableaux, indépendamment du calcul du ou exclusif, on a affaire à un cas particulier de la fonction `map` qui consiste à appliquer une fonction donnée à chaque élément d'un ou plusieurs tableaux, en combinant les éléments de même rang. ```python >>> list(map(operator.xor, [1, 0, 1], [1, 1, 0])) [0, 1, 1] >>> list(map(operator.add, [1, 2, 3, 4], [5, 6, 10, -4])) [6, 8, 13, 0] ``` Le schéma qui consiste à appliquer une même opération à chacun des éléments d'une liste est tellement fréquent que Python fournit la syntaxe spécifique des listes en compréhension pour l'exprimer : `[f(x) for x in liste]` est équivalent à `map(f, liste)`. L'utilisation de `assert` dans l'énoncé est discutable. En effet, cette instruction, qui est bien au programme de NSI, est préconisée pour le prototypage d'une fonction afin de garantir des préconditions sur les arguments et des postconditions sur les résultats. L'illustration d'une spécification au moyen de tests se fait plutôt au moyen des *doctests* de Python, ceux-ci font partie des pratiques établies et bénéficient d'un outillage par le langage. ### Suggestions Extensions envisageables, questions que l'on peut poser - produire la liste des indices où les listes ne coïncident pas. On oblige alors la création dynamique de la liste résultat dont la longueur sera fonction des valeurs des paramètres. La manipulation de listes d'indices est un savoir-faire souhaitable. - changer l'opérateur "ou exclusif" pour un autre, par exemple le produit d'entiers. Cet opérateur pourrait même être défini par une fonction. L'exercice consiste alors à écrire la fonction `map()`. - que se passe-t-il si on passe des listes de tailles différentes ? Pourquoi l'énoncé donne-t-il comme prérequis l'égalité des longeurs des tableaux ? Reformulation possible de l'énoncé : :::warning L'opérateur « ou exclusif », entre deux bits, produit 0 si les deux bits sont égaux et 1 s'ils sont différents : 0 ⊕ 0 = 0 , 0 ⊕ 1 = 1 , 1 ⊕ 0 = 1 , 1 ⊕ 1 = 0 On représente ici une suite de bits par un tableau contenant des 0 et des 1. Exemples : ```python a = [1, 0, 1, 0, 1, 1, 0, 1] b = [0, 1, 1, 1, 0, 1, 0, 0] c = [1, 1, 0, 1] d = [0, 0, 1, 1] ``` Écrire une fonction `xor` qui prend en entrée deux tableaux de même longueur contenant des 0 et des 1 et qui renvoie un tableau de même longueur que les entrées. Dans le tableau résultat, l’élément d'indice `i` est le résultat du « ou exclusif » appliqué aux éléments de même indice des tableaux passés en entrée. Les doctests suivants permettent de valider la fonction : ```python def xor(a, b): """ >>> a = [1, 0, 1, 0, 1, 1, 0, 1] >>> b = [0, 1, 1, 1, 0, 1, 0, 0] >>> c = [1, 1, 0, 1] >>> d = [0, 0, 1, 1] >>> xor(a, b) [1, 1, 0, 1, 1, 0, 0, 1] >>> xor(c, d) [1, 1, 1, 0] """ ... return ... ``` ::: ## Exercice 2 **Mots-clés :** programmation orientée objet, tableaux à deux dimensions. ### Énoncé :::info EXERCICE 2 (4 points) Dans cet exercice, on appelle carré d’ordre $n$ un tableau de $n$ lignes et $n$ colonnes dont chaque case contient un entier naturel. 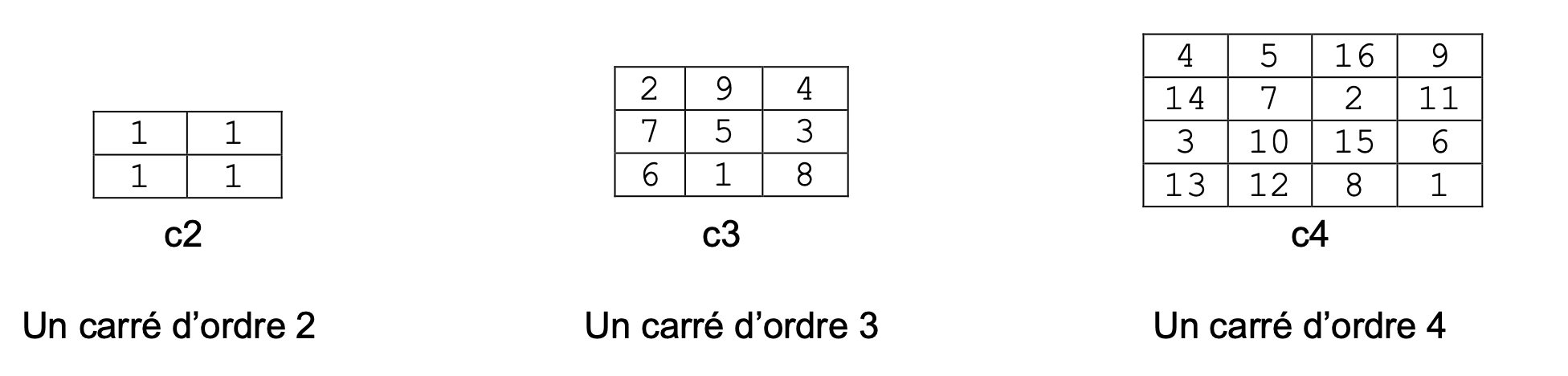Exemples :  Un carré est dit magique lorsque les sommes des éléments situés sur chaque ligne, chaque colonne et chaque diagonale sont égales. Ainsi c2 et c3 sont magiques car la somme de chaque ligne, chaque colonne et chaque diagonale est égale à 2 pour c2 et 15 pour c3. c4 n’est pas magique car la somme de la première ligne est égale à 34 alors que celle de la dernière colonne est égale à 27. La classe `Carre` ci-après contient des méthodes qui permettent de manipuler des carrés. Compléter la fonction `est_magique` qui prend en paramètre un carré et qui renvoie la valeur de la somme si ce carré est magique, `False` sinon. ```python class Carre: def __init__(self, tableau = [[]]): self.ordre = len(tableau) self.valeurs = tableau def affiche(self): '''Affiche un carré''' for i in range(self.ordre): print(self.valeurs[i]) def somme_ligne(self, i): '''Calcule la somme des valeurs de la ligne i''' return sum(self.valeurs[i]) def somme_col(self, j): '''calcule la somme des valeurs de la colonne j''' return sum([self.valeurs[i][j] for i in range(self.ordre)]) def est_magique(carre): n = carre.ordre s = carre.somme_ligne(0) #test de la somme de chaque ligne for i in range(..., ...): if carre.somme_ligne(i) != s: return ... #test de la somme de chaque colonne for j in range(n): if ... != s: return False #test de la somme de chaque diagonale if sum([carre.valeurs[...][...] for k in range(n)]) != s: return False if sum([carre.valeurs[k][n-1-k] for k in range(n)]) != s: return False return ... ``` Tester la fonction `est_magique` sur les carrés `c2`, `c3` et `c4`. ::: ### Propositions de solutions ```python def est_magique(carre): n = carre.ordre s = carre.somme_ligne(0) #test de la somme de chaque ligne for i in range(1, n): if carre.somme_ligne(i) != s: return False #test de la somme de chaque colonne for j in range(n): if carre.somme_col(j) != s: return False #test de la somme de chaque diagonale if sum([carre.valeurs[k][k] for k in range(n)]) != s: return False if sum([carre.valeurs[k][n-1-k] for k in range(n)]) != s: return False return s ``` Et le test de la fonction sur les trois carrés donnés en exemple : ```python c2 = Carre([[1, 1], [1,1]]) c3 = Carre([[2, 9, 4], [7, 5, 3], [6, 1, 8]]) c4 = Carre([[4, 5, 16, 9], [14, 7, 2, 11], [3, 10, 15, 6], [13, 12, 8, 1]]) >>> est_magique(c2) 2 >>> est_magique(c3) 15 >>> est_magique(c4) False ``` ### Analyse Cet exercice porte sur la manipulation de tableaux à 2 dimensions, l'utilisation de classes fournies et la création d'objets. On notera l'utilisation de listes en compréhension, et du `range` avec deux paramètres. Plusieurs aspects sont discutables. La représentation des carrés, tableaux à deux dimensions, par des tableaux de tableaux est implicite et seulement suggérée par la forme de l'argument par défaut dans le constructeur de la classe `Carre` et par la forme de l'indexation dans le code fourni. Même si la représentation des matrices sous cette forme fait partie des attendus du programme, le sujet devrait préciser la représentation utilisée pour les carrés. L'argument par défaut dans le constructeur de la classe `Carre` est un tableau à 1 ligne et 0 colonne, ce qui ne correspond pas à un carré. Par ailleurs, donner une valeur par défaut n'a pas de sens par rapport au problème, il serait préférable de ne pas en mettre du tout. L'exercice propose d'écrire une fonction acceptant un unique paramètre de la classe `Carre`. Une telle fonction est naturellement à définir comme une méthode de la classe. Rien ne justifie le choix de l'énoncé. Un autre aspect relatif à la programmation objet est l'utilisation maladroite d'un attribut de la classe, qui plus est dans une fonction – et pas une méthode. La pratique est de définir une méthode pour accéder à une telle valeur. La fonction à définir renvoie des valeurs de types différents selon les paramètres. Cette pratique va à l'encontre même de la notion de fonction dont le résultat est voué à être réutilisé. Une autre possibilité est de définir deux fonctions : une fonction qui teste si le carré est magique, et une fonction qui renvoie la somme d'un carré magique (par un unique appel à la méthode `somme_ligne()`). Une troisième possibilité est de renvoyer un couple de valeurs : le booléen et la somme. D'autres points de moindre importance peuvent être relevés : * Les documentations des méthodes ne respectent pas strictement les usages établis. * Il n'est pas attendu que les élèves soient familiers avec l'utilisation de la fonction prédéfinie `sum()`. * Marginalement la phrase qui débute par « c4 n’est pas ... » perturbe la lecture. On aurait pu écrire « Le carré `c4` n'est pas... ». ### Suggestions On ajoute dans l'énoncé : * les carrés sont représentés par des listes de listes d'entiers * la fonction prédéfinie `sum()` renvoie la somme des éléments d'une liste de nombres. Une version du code à compléter prenant en compte les remarques précédente pourrait être : ```python class Carre: def __init__(self, tableau): '''Crée une instance de Carre à partir d'un tableau à deux dimensions. Le tableau est supposé carré et non vide.''' self.ordre = len(tableau) self.valeurs = tableau def affiche(self): '''Affiche le carré.''' for i in range(self.ordre): print(self.valeurs[i]) def somme_ligne(self, i): '''Renvoie la somme des valeurs de la ligne i.''' return sum(self.valeurs[i]) def somme_col(self, j): '''Renvoie la somme des valeurs de la colonne j.''' return sum([self.valeurs[i][j] for i in range(self.ordre)]) def est_magique(self): '''Renvoie True si le carré est magique, False sinon.''' n = self.ordre s = self.somme_ligne(0) # test de la somme de chaque ligne for i in range(..., ...): if self.somme_ligne(i) != s: return ... # test de la somme de chaque colonne for j in range(n): if ... != s: return False # test de la somme de chaque diagonale if sum([self.valeurs[...][...] for k in range(n)]) != s: return False if sum([self.valeurs[k][n - 1 - k] for k in range(n)]) != s: return False return ... def somme(self): '''Renvoie la somme du carré. Le carré doit être magique.''' return ... ``` Le test du code complété sera alors par exemple : ```python c2 = Carre([[1, 1], [1, 1]]) c3 = Carre([[2, 9, 4], [7, 5, 3], [6, 1, 8]]) c4 = Carre([[4, 5, 16, 9], [14, 7, 2, 11], [3, 10, 15, 6], [13, 12, 8, 1]]) >>> c2.est_magique() True >>> c2.somme() 2 >>> c3.est_magique() True >>> c3.somme() 15 >>> c4.est_magique() False ``` On se gardera bien de faire un appel `c4.somme()`. De possibles questions pour l'oral sont * de questionner la représentation en ligne ou en colonne du carré * de proposer de remplacer le `range(1, n)` par `range(n)` * de proposer une version avec un unique `return` terminal de la méthode `est_magique()` * de supprimer l'attribut `ordre` et d'ajouter une méthode `ordre()` ### Conclusion Un exercice de compréhension de la programmation objet, sans autre enjeu ou ouverture, qui mériterait d'être amendé.