--- title: VISI601_CMI TP2 Equations de diffusion et débruitage d'image --- # TP2 - Equations de diffusion et débruitage d'image > [name=Jacques-Olivier Lachaud][time=February 2022][color=#907bf7][time=March 2023][color=#907bf7] > (Les images peuvent être soumises à des droits d'auteur. Elles sont utilisées ici exclusivement dans un but pédagogique) ###### tags: `visi601` `tp` Retour à [VISI601_CMI (Main) Algorithmique numérique](https://codimd.math.cnrs.fr/s/IWTaBkA9m) --- [TOC] --- :::warning Archive d'images à récupérer (mise à jour du 14/3/2023) : [Data2.zip](https://jacquesolivierlachaud.github.io/lectures/info601cmi/Cours/Data2.zip) Le répertoire principal contient les images originales. Le répertoire `Noisy` contient des versions bruitées de ces images, avec un bruit plus ou moins intense. ::: --- ## Introduction Ce TP vous fait travailler la résolution d'équations de diffusion, c'est-à-dire des équations aux dérivées partielles faisant intervenir le Laplacien de la fonction. On rappelle qu'en coordonnées cartésiennes le Laplacien de $u$ est la somme de ses dérivées secondes: $\Delta u = \partial_{xx} u + \partial_{yy} u$. On peut aussi le définir de façon plus générale comme la divergence du gradient de $u$, i.e. $\Delta u := \mathrm{div}( \nabla u )$. Cet opérateur intervient dans un grand nombre de problèmes et d'équations. On peut citer par exemple: - équation de Laplace: $\Delta u = 0$ (Théoriquement, les solutions, dites harmoniques, sont les fonctions holomorphes sur les complexes.) - équation de Poisson: $\Delta u = f$ + conditions aux bords (problème statique d’une membrane élastique tendue et chargée (une peau de tambour)) - débruitage d'une image $I$ : $\mathrm{argmin}\,E(u) = \int_\Omega \alpha |u-I|^2 + |\nabla u |^2$ - diffusion isotrope/anisotrope: $\partial_t u = \mathrm{div}( c \nabla u )$ - calcul de géodésiques et de la fonction distance $d$ - intégrer le flot de chaleur $\partial_t u = \Delta u$ pour un temps t, - évaluer le champ de vecteur $X = − \nabla u / |\nabla u|$, - résoudre l'équation de Poisson $\Delta d = \nabla \cdot X$. - reconstruction de surfaces à partir de nuages de points P munis de normales N: - Résoudre l'équation de Poisson $\Delta \phi = \nabla \cdot N$. :::info On va chercher à éliminer du bruit ou des imperfections sur les images. La méthode va être de résoudre des problèmes de diffusion simple dans une grille. ::: Vous trouverez beaucoup de documentation utile sur python et numpy à ces adresses: - python (v3): https://docs.python.org/3/ - numpy: https://docs.scipy.org/doc/numpy/reference/routines.html - scipy: https://docs.scipy.org/doc/scipy/reference/ - numpy.linalg: https://docs.scipy.org/doc/numpy/reference/routines.linalg.html **A rendre** : Vous me ferez une archive contenant le ou les programmes python, ainsi qu'un compte-rendu donnant l'état d'avancement et les différentes choses demandées dans l'énoncé. Il sera tenu compte dans la notation du respect des consignes, de la qualité de code, mais aussi de la façon dont chaque partie du travail demandé est testée (dans le compte-rendu ou dans le code lui-même). Vous me remettrez l'archive via <a href="https://tplab.apps.math.cnrs.fr">TPLab</a>. , en fin de séance, puis une version finale avant le **dimanche 31 mars, minuit** ## I Construction de l'opérateur Laplacien Les équations que nous allons résoudre se formulent dans un domaine continu $\Omega \subset \mathbf{R}^2$, que l'on prend souvent rectangulaire, mais nous allons devoir les discrétiser pour obtenir des solutions numériques. Cela va se traduire par la création de systèmes linéaires assez grands. On a vu au TP précédent que les représentations denses de matrices ne seront pas efficaces. On va donc utiliser des matrices creuses. ### I.1 Une classe Grid pour représenter le domaine Pour simplifier le code, une classe va représenter une grille avec `nbrow` lignes et `nbcol` colonnes. Voilà un squelette de la classe. ```python= import numpy as np from scipy.sparse import * import matplotlib.pyplot as plt import matplotlib.image as mpimg class Grid: """ Constructeur. Fabrique une grille avec `nbrow` lignes et `nbcol` colonnes. """ def __init__( self, nbrow, nbcol ): self.nbcol = nbcol self.nbrow = nbrow self.number() """ Numérote les pixels dans le dictionnaire `self.index`, et pour un index `idx` mémorise sa ligne `self.I[ idx ]` et sa colonne `self.J[ idx ]` """ def number( self ): self.I = [i for i in range(self.nbrow) for j in range(self.nbcol)] self.J = [j for i in range(self.nbrow) for j in range(self.nbcol)] self.index={} ... # A compléter pour index: (i,j) -> idx = i*nbcol+j """ Retourne le numéro/indice du pixel `(i,j)` ou -1 si pixel non trouvé. """ def getIndex( self, i,j ): return self.index.get( (i,j), -1 ) """ Retourne la ligne du pixel d'indice `idx` """ def getRow( self, idx ): return self.I[ idx ] """ Retourne la colonne du pixel d'indice `idx` """ def getCol( self, idx ): return self.J[ idx ] ``` > Cette classe nous facilitera la création des opérateurs Laplacien, mais aussi dans le TP suivant, permettra de gérer facilement des domaines non rectangulaires et d'autres opérateurs. [color=#907bf7] On va numéroter les cases de la grille de 0 à `nbrow*nbcol-1`, dans l'ordre `(0,0),(0,1),...`. Ainsi la méthode `number` crée deux tableaux donnant les lignes (`self.I`) et colonnes (`self.J`) pour chacun des indices possibles. :::info **Complétez** la méthode `self.number` pour qu'elle fabrique le dictionnaire `self.index` qui va permettre de passer de coordonnées `(i,j)` à l'indice d'une case de la grille. ::: Si on crée un domaine de 3 lignes et 4 colonnes, alors ça devrait afficher ```python= D = Grid( 3, 4 ) print(D.J) print(D.I) print(D.index) ``` ```shell [0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3] [0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2] {(0, 0): 0, (0, 1): 1, (0, 2): 2, (0, 3): 3, (1, 0): 4, (1, 1): 5, (1, 2): 6, (1, 3): 7, (2, 0): 8, (2, 1): 9, (2, 2): 10, (2, 3): 11} ``` ### I.2 Voisins dans la grille On vous a donné la méthode `getIndex` qui permet de retrouver l'index d'une case `(i,j)` ou `-1` si la case est en dehors de la grille. :::info Ecrivez alors la méthode `neighbors(idx)` qui retourne la liste des indices des voisins directs du sommet d'indice `idx`. ```python= def neighbors( self, idx ): N=[] ... return N ``` ::: On note qu'une case peut avoir 2, 3 ou 4 voisins directs. > L'idée est de retrouver les coordonnées (i,j) à partir de `idx`, tester si les 4 voisins (i+1,j), ..., existent et si oui, d'ajouter leur indice à N, avec `N.append(...)`. ### I.3 Construction de l'opérateur Laplacien Si on note $u_{i,j} := u( i h, j h )$ les valeurs de la fonction $u$ sur les noeuds de la grille, avec $h$ l'écartement spatial entre les noeuds, on peut approcher l'opérateur Laplacien ainsi: $$ L(u_{i,j}) := \frac{1}{h^2}\left( u_{i+1,j} + u_{i-1,j} + u_{i,j+1} + u_{i,j-1} - 4u_{i,j} \right). $$ On va ici simplement supposer que $h=1$. Si on écrit $u_{i,j}$ sous forme d'un vecteur en utilisant l'index de `(i,j)` dans la grille, la relation précédente peut s'écrire sous forme matricielle. La ligne `index(i,j)` de la matrice L représentant le Laplacien devient: $$ \begin{bmatrix}0 &\cdots& 0& 1& 0& \cdots& 0& 1& -4& 1& 0& \cdots& 0& 1& 0& \cdots& 0& \end{bmatrix} $$ où les 1 sont sur les colones `index(i,j-1)`, `index(i-1,j)`, etc, et le -4 est sur la diagonale. Pour obtenir le Laplacien de la fonction $u$, il suffira d'écrire le vecteur colonne $\mathbf{u}$ de ses valeurs (dans l'ordre des indices) et de faire le produit matrice/vecteur $L \mathbf{u}$. :::info Inspirez-vous de la méthode `Identity` ci-dessous, pour écrire la méthode `Laplacian` qui calcule et retourne la matrice creuse $L$ du Laplacien discret. ::: ```python= # dans class Grid """ Taille n du vecteur u. """ def size(self): return len(self.I) """ Retourne la matrice identité de taille nxn """ def Identity(self): n = self.size() LIGS = [] # les lignes des coefficients COLS = [] # les colonnes des coefficients VALS = [] # les valeurs des coefficients for idx in self.index.values(): LIGS.append( idx ) COLS.append( idx ) VALS.append( 1.0 ) M = coo_matrix( (VALS,(LIGS,COLS)), shape = (n,n) ) return M.tocsc() ``` :::warning > Attention aux coefficients que vous mettez aux **bords** du domaine. Suivant les choix, vous imposez des conditions de Dirichlet nulle aux bords (en gardant le coefficient -4 aux bords sur la diagonale) ou des conditions de Neumann (en mettant le coefficient `-nbvoisins(i,j)` sur la diagonale). Vous écrirez deux méthodes `LaplacianD` (pour Dirichlet) et `Laplacian` tout court pour Neumann, plus naturel ici. ::: ## II Processus de diffusion ### II.1 Diffusion simple par Euler explicite On veut maintenant faire un processus de diffusion simple: $$ \partial_t u = \Delta u,\quad \text{avec}\quad u(x,y,0) = u_0(x,y) $$ On peut discrétiser cette équation avec la méthode d'Euler explicite. Si on note $\mathbf{u}^{(k)}$ la valeur de $\mathbf{u}$ au temps $k \delta t$, avec $\delta t$ le pas de temps, alors la version discrétisée peut s'écrire: $$ \underbrace{\frac{\mathbf{u}^{(k+1)}-\mathbf{u}^{(k)}}{\delta t}}_{\text{dérivée "forward"}} = L \mathbf{u}^{(k)} $$ avec $L$ la matrice discrétisant l'opérateur Laplacien $\Delta$, ou en notant $\mathrm{Id}$ la matrice identité: $$ \mathbf{u}^{(k+1)} = \left( \mathrm{Id} + \delta t L \right) \mathbf{u}^{(k)} $$ :::info Il ne reste plus qu'à écrire la méthode `explicitEuler( U0, T, dt )` de `Grid` qui calcule la valeur de U au temps T en itérant l'équation précédente par pas de `dt` au maximum. ```python= # dans la classe Grid """ A partir du vecteur de valeurs U0, calcule U(T) en itérant des pas dt successifs. """ def explicitEuler( self, U0, T, dt ): # à écrire ... ``` ::: Le bout de code suivant permet de transformer un vecteur en une image et d'afficher l'image. ```python= # dans class Grid def vectorToImage(self, V ): img = np.zeros( (self.nbrow, self.nbcol) ) K = self.index.keys() I = self.index.values() for k,idx in zip(K,I): img[k[0],k[1]] = V[idx] return img ... D = Grid( 10, 10 ) V = [0.] * D.size() V[42] = 5.0 V[37] = 10.0 # F it 20 itérations de pas 0.1 pour arriver au temps 2 V = D.explicitEuler( V, 2.0, 0.1 ) img = D.vectorToImage( V ) plt.imshow(img,cmap='hot',vmin=0.0,vmax=1.0) ``` | 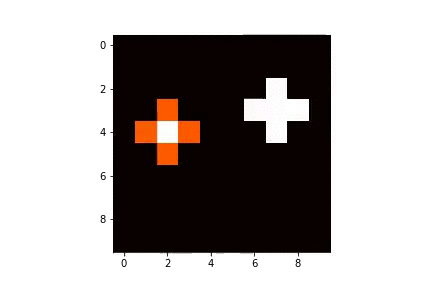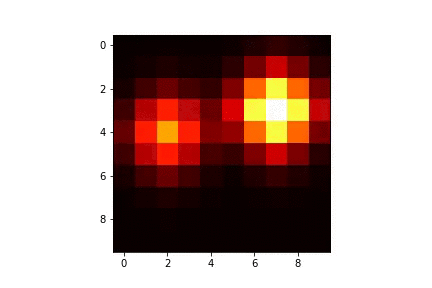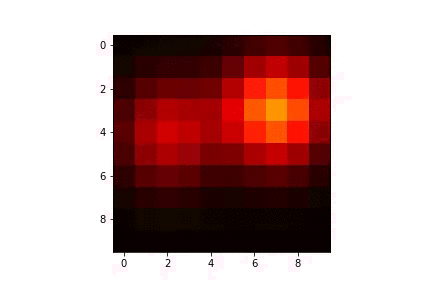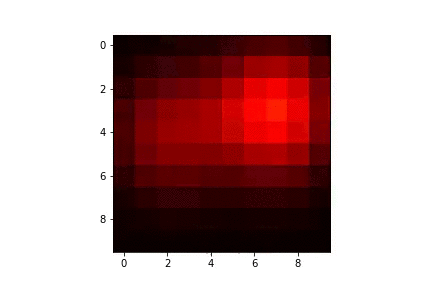 | | -------- | | Diffusion par méthode d'Euler explicite à partir de deux sources | > La page [Images en Python](https://codimd.math.cnrs.fr/s/uatRBXalq) peut être utile. :::warning > Essayez d'augmenter le pas `dt` pour faire moins d'itérations. Que remarquez-vous ? [color=#907bf7] ::: ```python= # Pour ceux qui veulent faire un film ! import matplotlib.animation as animation fig = plt.figure() ims = [] for i in range(20): V += 0.1*L*V img = D.vectorToImage( V ) im = plt.imshow(img,cmap='hot',vmin=0.0,vmax=1.0, animated=True) ims.append([im]) ani = animation.ArtistAnimation(fig, ims, interval=50, blit=True, repeat_delay=1000) ani.save("movie.mp4") plt.show() ``` ### II.2 Diffusion simple par Euler implicite Plutôt que de considérer $\mathbf{u}^{(k)}$ pour calculer la diffusion au temps $t$, on peut considérer d'utiliser $\mathbf{u}^{(k+1)}$. Cela donne : $$ \frac{\mathbf{u}^{(k+1)}-\mathbf{u}^{(k)}}{\delta t} = \underbrace{L \mathbf{u}^{(k+1)}}_{\text{Laplacien après mouvement !}} $$ ce qui se réécrit ainsi : $$ \left( \mathrm{Id} - \delta t L \right) \mathbf{u}^{(k+1)} = \mathbf{u}^{(k)} $$ Il s'agit d'un système linéaire creux de la forme $A \mathbf{x} = \mathbf{b}$. On montre de plus qu'il est inconditionnellement stable pour $\delta t>0$. On peut donc tout de suite calculer le résultat au temps `T` par une décomposition LU (même Cholesky car la matrice est symmétrique). :::info Ecrivez la méthode `implicitEuler( self, U0, T, dt )` qui fait ce calcul. Utilisez `scipy.sparse.linalg.splu`. ::: > Essayez d'augmenter le pas `dt` pour faire moins d'itérations. Que remarquez-vous ? Est-ce différent de la méthode d'Euler explicite ?[color=#907bf7] > `dt` peut être choisi plus grand dans Euler implicite que Euler explicite, mais néanmoins la précision est de l'ordre de $O(dt+h^2)$. [color=#cc0000] ### II.3 Diffusion sur une image > La page [Images en Python](https://codimd.math.cnrs.fr/s/uatRBXalq) peut être utile. On va appliquer le même principe de diffusion sur une image. Le code suivant charge une image dans un tableau `numpy.array`. Attention, une image a trois composantes couleur (rouge, vert, bleu). On les obtient ainsi : ```python= img=mpimg.imread('Noisy/mandrill-g01.png') plt.imshow(img) # image couleur red = img[:, :, 0] green = img[:, :, 1] blue = img[:, :, 2] # Par exemple, on peut afficher son canal rouge en niveau de gris imgplot = plt.imshow(red,cmap='gray',vmax=1.0,vmin=0.0) # plt.show() si nécessaire pour l'affichage ``` |  | | | -------- | -------- | | mandrill 240x240 bruité | son canal rouge | Ecrivez la méthode `imageToVector(self, img)` qui transforme une image en un vecteur, puis appliquer le processus de diffusion précédent sur chaque composante. Reconstruisez les trois composantes obtenues sous forme d'une image couleur. ```python= """ A partir d'une image N&B Img, diffuse cette image pendant un temps T, par pas dt, et retourne l'image résultante """ def diffuseImage( Img, T, dt ): ... """ A partir d'une image couleur Img, diffuse chaque canal de cette image pendant un temps T, par pas dt, et retourne l'image couleur résultante """ def diffuseImageRGB( Img, T, dt ): ... ``` Vous devriez obtenir les résultats suivants, à partir d'image ci-dessus (mandrill 240x240 bruité). |  |  | | ------------------------------------------------------------------------------------------------------------------------------- | ---------------------------------------------------------------------------------------------------------------------------- | | Après diffusion isotrope T=5 (Euler implicite, Dirichlet conditions, dt=0.5) | Après diffusion isotrope T=5 (Euler implicite, Neumann conditions, dt=0.5) | :::warning Observez à gauche le noir qui se propage des bords de l'image : vous avez utilisé le Laplacien de Dirichlet qui suppose/impose une valeur nulle de l'image en dehors du domaine, qui se diffuse au cours du temps. Au contraire à droite, les conditions de Neumann imposent juste une propagation des valeurs du bord à l'extérieur du domaine. ::: ### II.4 Diffusion comme minimisation d'une fonctionnelle On voit que diffuser l'image élimine le bruit mais élimine les détails aussi. En fait, on peut interpréter la diffusion précédente comme un équilibre énergétique entre la fidélité aux données (ici l'image $I$) et un terme qui évite les variations trop brusques de l'image reconstruite $u$ (donc les forts gradients, typiques du bruit). On cherche donc $$ \mathrm{argmin}\, E(u) = \int_\Omega |u-I|^2 + \alpha \int_\Omega | \nabla u |^2 $$ Une condition nécessaire (et suffisante ici) pour minimiser la fonctionnelle précédente est que sa première variation soit nulle (équation d'Euler-Lagrange). Cela s'écrit: $$ \forall (x,y) \in \Omega, 2 (u(x,y)-I(x,y)) - 2 \alpha \Delta u(x,y) = 0 $$ Cette équation est valable sur tout le domaine $\Omega$. On la discrétise sur les pixels, et on approche le Laplacien $\Delta$ par notre matrice $L$. Il vient: $$ (\mathrm{Id} - \alpha L) \mathbf{u} = \mathbf{I} $$ Et on reconnait la diffusion de l'image $\mathbf{I}$ par l'équation d'Euler implicite pour le temps $T=\alpha$. Un gros $\alpha$ relâche l'attache aux données et implique une forte diffusion. Cela nous dit aussi qu'il existe un $\alpha^*$ optimal pour un bruit donné. Si on sait qu'un bruit de variance $\sigma^2$ a perturbé l'image, alors $\int_\Omega |u^*-I|^2 \approx \mathrm{Aire}(\Omega) 3\sigma^2$ autour de l'optimum $u^*$ (le 3 vient des 3 canaux R,G,B). On prend donc $\alpha$ proportionnel à $\sigma^2$ pour contrebalancer cet effet, néanmoins la constante de proportionnalité dépend de l'intensité et du contraste moyen de l'image (bref, faites des essais !). On vous donne dans l'archive des images originelles et bruitées. Calculez les variances dans les différents cas puis débruitez les images correspondantes. Pour mesurer la qualité du débruitage, on peut utiliser la mesure signal/bruit (dite PSNR). Si $\mathbf{u}$ est une image et $\mathbf{g}$ est l'image originelle, alors le PSNR est défini ainsi: $$ \begin{align*} PSNR &= 10 \log_{10}(v^2/EQM),\\ EQM &= 1/(3N) \sum_i \| \mathbf{u}(x_i,y_i) - \mathbf{g}(x_i,y_i) \|^2 \end{align*} $$ où $v$ est la **valeur maximale** dans l'image et le 3 vient du fait qu'il y a trois canaux rouge, vert, bleu. Plus le PSNR est élevé plus $\mathbf{u}$ est proche de $\mathbf{g}$ (il est infini si le débruitage est parfait: $\mathbf{u}=\mathbf{g}$). :::info Vérifiez que vous trouvez bien les valeurs optimales ci-dessous vis-à-vis du PSNR pour les images "mandrill-g01" et "mandrill-g02", en traçant les courbes du PSNR en fonction de la diffusion $\alpha$. ::: > Vous écrirez des méthodes `EQM(u,g)`, puis `PSNR(u,g)` et `PSNR_RGB(u,g)` puis vous pouvez tracer la qualité du débruitage par diffusion en fonction de différentes valeurs de T. Voilà un exemple de tracé de PSNR en fonction du temps de diffusion. Vous afficherez aussi le meilleur débruitage obtenu. |  |  | | ------------------------------------------------------------------------------------------------------------------------------------------------------- | --- | | PSNR en fonction du temps de diffusion (i.e. $\alpha$) sur l'image `mandrill-g01.png`. Ici 0.3 semble proche de l'optimal, avec un PSNR proche de 25.5. | PSNR en fonction du temps de diffusion (i.e. $\alpha$) sur l'image `mandrill-g02.png`. Ici 0.6 semble proche de l'optimal, avec un PSNR proche de 22.7. | :::info En utilisant la même approche que ci-dessus, restaurez les différentes images du répertoire `Noisy`. Evidemment on triche ici puisqu'on connait l'image originelle, et donc qu'on peut trouver une diffusion optimale. ::: | |  | | -------- | -------- | | lighthouse bruité $\sigma=0.025$ | restauration $\alpha=0.45$ | ## Pour aller un peu plus loin Il s'agit ici d'un modèle variationnel très simple de débruitage d'image, mais il a conduit à développer de nombreux autres modèles variationnels sur les mêmes principes, les plus connus étant: - le modèle de diffusion anisotrope, qui diffuse différemment en fonction du contraste local. Il se résoud assez simplement avec un schéma proche d'un Euler explicite. - le modèle de variation totale (TV) et ses nombreuses variantes (GTV*) : on pénalise plutôt $| \nabla u |$ (ou des variantes) plutôt que $|\nabla u|^2$. Il met en jeu des algorithmes plus complexes d'optimisation. - le modèle de Mumford and Shah, et ses relaxations calculables comme le modèle d'Ambrosio-Tortorelli, qui cherche des approximations lisses par morceaux pour débruiter ou segmenter les images.