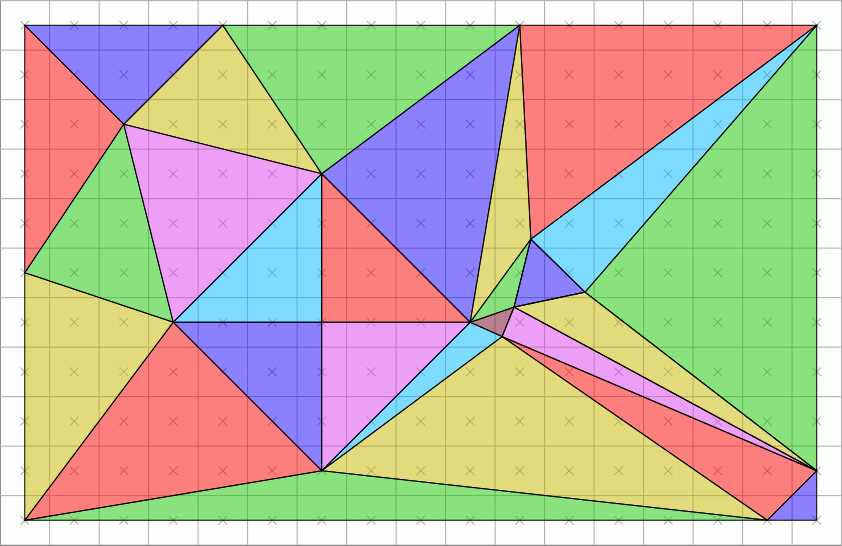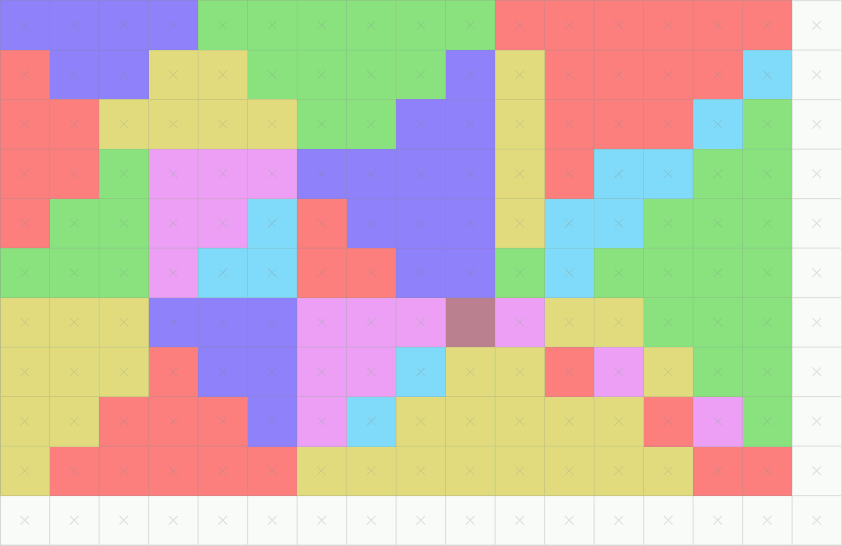[CGDI] Rasterization, z-Buffer and Winding Numbers === > [name="David Coeurjolly"] ENS [CGDI](https://perso.liris.cnrs.fr/vincent.nivoliers/cgdi/) Version [TOC] --- The objective of the practical is to play with basic 2D geometrical predicates illustrated using the [rasterization](https://en.wikipedia.org/wiki/Rasterisation) problem. ([wikipedia](https://commons.wikimedia.org/wiki/File:Top-left_triangle_rasterization_rule.gif)) The initial problem is quite simple: Given a triangle $\mathcal{T}$ in the plane (with vertices in $\mathbb{R}^3$), we want to construct the set of grid points $T$ such that $T:= D(\mathcal{T}):=\mathcal{T}\cap \mathbb{Z}^2$. # Rasterization of triangles :::danger There is no special code for this practical in `python`, just use the python code snippet to export an image from the previous practicals. ::: ## Playing with the orientation predicate From the lecture notes, given threep points $p,q,r\in\mathbb{R}^2$, we can design a simple determinant test to decide if $r$ lies on the *left*, on the *right*, or on the (oriented) straight line $(pq)$.  This can be done by considering an $Orientation(p,q,r)$ predicate defined as the sign of the determinant of $(\vec{pq}, \vec{pr})$ (aka the **signed** area of the parallelogram defined by $\vec{pq}$ and $\vec{pr}$). 1. Set up a rasterization project to implement the following problem: Given an image $[0,width]\times[0,height]$, a triangle $\mathcal{T}$ in that domain, we would like to highlight the pixels **inside or on** $\mathcal{T}$. 2. From the orientation predicate, how can you implement a `isInside(p,q,r,pixel)->{true, false}` predicate? Implement such function for a single triangle T and use it to solve the initial rasterization problem. :::info **Hint:** Make sure to have edges of $\mathcal{T}$ properly oriented... ::: 3. For sure, `isInside(p,q,r,pixel)` should be in $O(1)$ and beside fancy sign of determinant computation tricks, there is very few thing you can do to optimize the process. However, to rasterize a complete triangle $\mathcal{T}$, can you imagine further optimization? 4. Now, we are considering a collection of triangles $\{\mathcal{T}_i\}_N$ (with a unique color per triangle). Obviously, we can loop on the function of the question 2, but what can you do to optimize the computations? 5. For two adjacent triangles $\mathcal{T}_1,\mathcal{T}_2$(ie. sharing an edge), do you have ${T}_1\cap {T}_2\neq\emptyset$ ? $D({\mathcal{T}_1\cup \mathcal{T}_2}) = T_1 \cup T_2$ ? Please experiment and comment. 6. Update a bit the `isInside(p,q,r,pixel)` function to also highlight pixel which lies exactly on an edge (e.g. use a different color for such points in the rasterization). :::warning Conservative vs. non-conservative raterization, and optimized code are important bottleneck issues in GPU designs. See for instance [nvidia](https://developer.nvidia.com/gpugems/gpugems2/part-v-image-oriented-computing/chapter-42-conservative-rasterization) notes. ::: 8. **Extra (Hurt Me Plenty.)** For an infinite straight-line $(pq)$ with $p,q\in\mathbb{R}^2$, what are the conditions for $p$ and $q$ to have $(pq)\cap\mathbb{Z}^2\neq \emptyset$? 9. **Extra (Ultra-Violence)** For $p\in\mathbb{Z}^2$, what are the solutions of $(Op)\cap\mathbb{Z}^2$. 10. **SuperExtra (Nightmare)** Given a 2D convex polygon with $N$ vertices, design a sub-linear "Point-in-Polygon" test. If the polygon is not convex (but *simple*), design a linear in time algorithm for the "Point-in-Polygon" test. ## Barycentric coordinates An alternative way to rasterize a triangle is to consider an area-based technique which is deeply linked to [barycentric coordinates](https://en.wikipedia.org/wiki/Barycentric_coordinate_system) for triangles. If $p$ lies inside the triangle $\mathcal{T}(a,b,c)$, then there is a unique barycentric formulation: $$p = \lambda_1 a + \lambda_2 b + \lambda_3 c$$ with $\lambda_i\geq 0$ and $\sum \lambda_i=1$. Barycentric weights are widely used in computer graphics to linearly interpolate vertex based value to points in $T$. For instance, if you attach colors to vertices, you define a linear blending as: $$color(p) = \lambda_1 color(a) + \lambda_2 color(b) + \lambda_3 color(c)$$ (as long as you have considered your color space as a linear vector space).  For triangles, barycentric coordinates can be easily computed from signed area as: $$\lambda_1=\frac{Area(cpb)}{Area(abc)},\quad \lambda_2=\frac{Area(apc)}{Area(abc)},\quad \lambda_3=\frac{Area(bpa)}{Area(abc)}\,.$$ Computing the $\lambda_i$ and checking whether they are all positive is a way to test if $p$ is inside $\mathcal{T}$ (this exacly corresponds to the test of the first section of this note). 10. Implement the barycentric coordinate method and interpolate colors using the barycentric linear blending. 11. Again, what can be done to design an as efficient as possible barycentric coordinate for triangle computation? ## The z-Buffer The [z-Buffer](https://en.wikipedia.org/wiki/Z-buffering) is one of the key ingredients in many realtime rendering techniques. Let us assume a set of triangles $\{\mathcal{T}_i\}$ with an $z$ component for the vertex coordinates. Such $z$ or *depth* components correspond to the projection of the 3D points into the 2D screen. We won't go into details here but keep in mind that changes of basis (from the 3d world to the camera frame) and the projection step (orthographic or pinhole according to the camera model) can be performed using a simple matrix/vector multiplication on homogeneous coordinates (cf the lecture). The **z-buffer** corresponds to an image buffer in which each pixel contains the depth (and the triangle id) of the closest triangle. The algorithm is pretty simple: Init a depth buffer with $+\infty$ values. For each triangle $\mathcal{T}_i$, raster $\mathcal{T}_i$ while interpolating the depth information from the vertices to inner pixels $p$, and store the depth information into an image keeping the closest triangle at that point (`zbuffer(p) = min( depth(p), zbuffer(p)` and the same for the triangle id). At the screen resolution, the z-buffer is a very efficient solution (usually baked in the graphic pipeline of GPUs) to solve the visibility issue of 3D projected triangles.  11. Implement a z-buffer using the barycentric coordinate rasterizer (random triangles with random depth values for the triangles). 12. Mix the linear color blending scheme with the z-buffer. # Winding numbers in 2D When dealing with more complex objects like non-simple polygonal curves (which may not be closed, with self-intersections, with multiple components..), defining and "inside" from an "outside" is a critical step in many computer graphics applications. Please refer to [^b1] and [^b2] for further details on the subject (and extensions to meshes and point cloud). On the smooth setting, the [winding number](https://en.wikipedia.org/wiki/Winding_number) at a point $p$ is the number of times the curve wraps around $p$ in the counter-clockwise direction: $$w(p)=\frac{1}{2\pi}\int_C d\theta\,.$$  If the winding number is zero, then $p$ is outside the curve. Otherwise, it is a integer index (for closed curve) accounting for the number of nested loops $p$ belongs to: [^b1] For open polygonal curve, $w(p)$ is not an integer anymore and can be computed by summing the solid angle at $p$: [^b1] $$w(p) = \frac{1}{2\pi}\sum_{i=1}^n \theta_i$$ The winding number map is now a smooth (harmonic) function that is zero, or close to zero outside, and which is positive inside. [^b1] 13. Express $\theta_i$ (or its tangent) from $p,c_i$ and $c_{i+1}$. 14. Given an open, non-simple polygonal object (sequence of vertices), write the function to export the Winding Number map (color map of the Winding Number at each point of a domain). # References [^b1]: Jacobson, A., Kavan, L., & Sorkine-Hornung, O. (2013). Robust inside-outside segmentation using generalized winding numbers. ACM Transactions on Graphics, 32(4). https://doi.org/10.1145/2461912.2461916 [^b2]: Barill, G., Dickson, N. G., Schmidt, R., Levin, D. I. W., & Jacobson, A. (2018). Fast winding numbers for soups and clouds. ACM Transactions on Graphics, 37(4). https://doi.org/10.1145/3197517.3201337