Samplers 101 == TP 1: https://codimd.math.cnrs.fr/s/eLBSMnqIg L'objectif de ce TP est de construire des échantillonneurs 2D classiques et d'évaluer leurs performances. ::: info **Prérequis**: * compilateur c/c++ classique * cmake récent * gnuplot :::  # Warmup 1. Récupérez le code du TP sur https://github.com/dcoeurjo/BenchSampling Pour l'évaluation des performances, deux outils sont possibles : [google benchmark](https://github.com/google/benchmark) (lib google pour du micro-benchmarking), ou alors une utilisation classique des [chronos c++](https://cplusplus.com/reference/chrono/) de la std. 2. Compilez le projet avec les exemples, eg.: :::success mkdir build cd build cmake .. 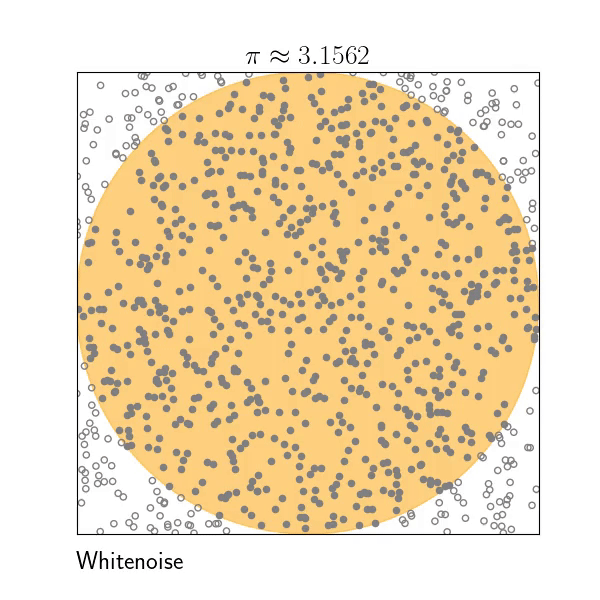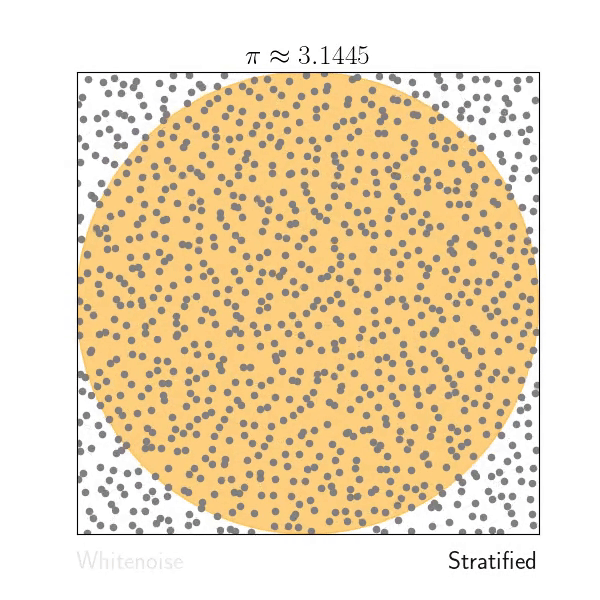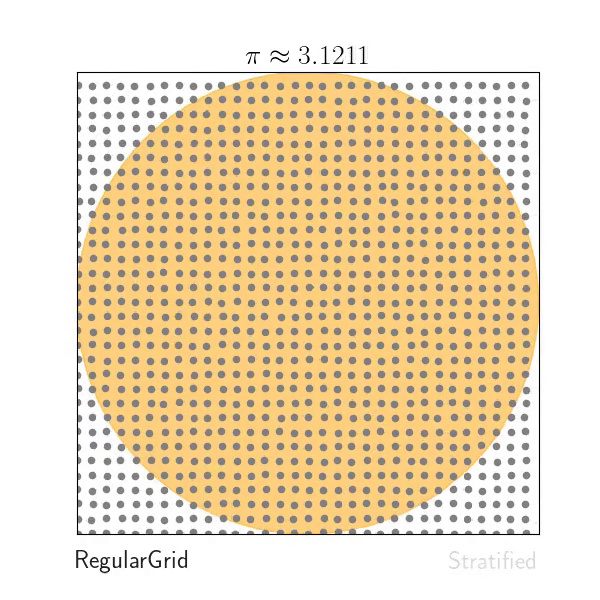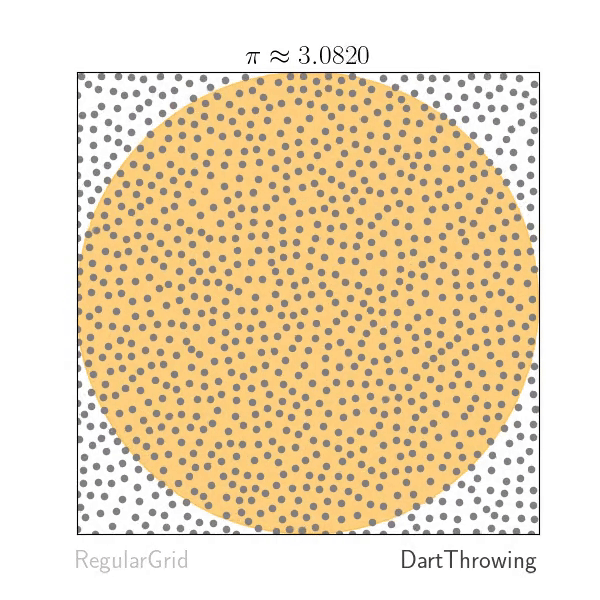::: 3. Regarder le squelette de code `whitenoise.cpp`, visualisez les échantillons avec `gnuplot` (ou autre) et completez celui-ci pour calculer un test d'intégration Monte-Carlo simple (eg. l'aire d'un disque unitaire centré dans $[O,1)^2$). :::warning :::spoiler Gnuplot tutorial Pour visualiser un ensemble de points en ASCII (un point par ligne, autant de colonnes que de dimensions), vous pouvez utiliser l'outil que vous voulez. Sous linux/macos, je vous conseille `gnuplot`. Dans un terminal, à l'endroit où le binaire `whitenoise` a été exécuté: * gnuplot puis * plot "WN-1024.pts" cela vous donne quelque chose comme cela:  Pour un test d'intégration Monte-Carlo (erreur en fonction du nombre d'échantillons), vous pouvez exporter vos données sous la forme ASCII suivante (les lignes avec # sont échappées): ``` #spp error 128 0.004 256 0.001 1024 0.0001 ... ``` Dans gnuplot, nous avons l'habitude de comparer les convergences en logscale. 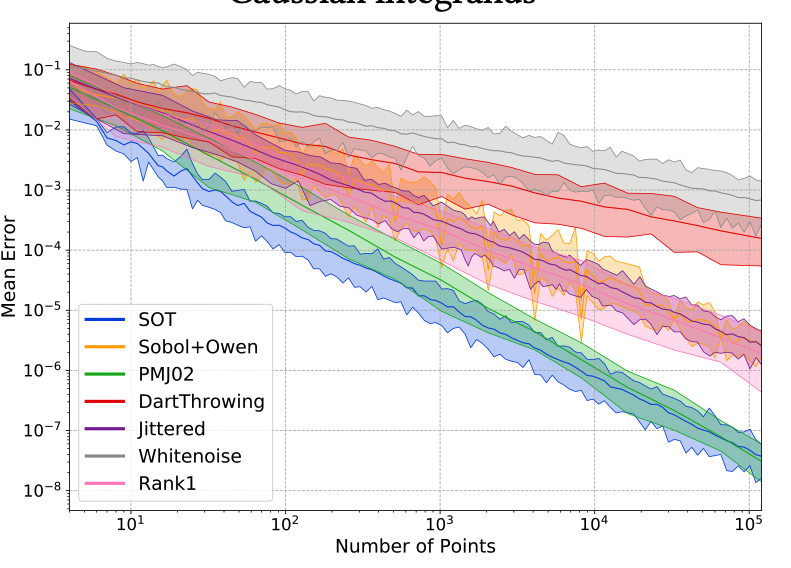Dans gnuplot: ``` set logscale plot "errors.txt" using 1:2 with line title "My great sampler", "previouswork.txt" using 1:2 with line "buggyprevious work" ``` avec un peu de tricks gnuplot, cela donne  : ::: :::warning :::spoiler Visualisation de points 2D Pour la visualisation de points 2d, `pts2svg` vous permet de convertir un fichier de points (ASCII, "x y") en SVG sachant un rayon de disque passé en paramètre (cf `--help`):  ::: :::warning ::: spoiler Visualisation de courbresde convergence Sous linux / macOS, l'approche la plus simple consiste à utiliser `gnuplot` en ligne de commande. Sous Windows, vous pouvez faire cette visualisation via `matplotlib` en `python`: ```python= import matplotlib.pyplot as pl import numpy as np data = np.loadtxt("WN_1024.pts") plt.scatter(data[:,0],data[:,1]) plt.show() ``` ```python= import matplotlib.pyplot as pl import numpy as np data = np.loadtxt("res_Strat.txt") data2 = np.loadtxt("res_WN.txt") plt.plot(data[:,0],data[:,1], label="Strat") plt.plot(data2[:,0],data2[:,1], label="WN") plt.yscale("log") plt.xscale("log") plt.legend() plt.show() ``` En dernier recours, vous pouvez utiliser Excel... ::: # Objectifs du TP Nous allons maintenant implémenter quelques échantillonneurs et les comparer dans un contexte d'intégration MC. L'évaluation des stratégies d'échantillonnage se fera sur la base : * de tests d'intégration * de tests de discrépance * de caractérisations spectrales Pour démarrer, utilisez le test d'intégration (aire disque unité) dans la section précédente. Par la suite, je vous propose de passer via les outils [utk](https://github.com/utk-team/utk) que nous découvrirons au cours de la séance.  Commencez par *Stratified Sampling*. On fera ensuite un survol d'[UTK](https://utk-team.github.io/utk/) et de ses outils. Par la suite, je vous propose de regarder Poisson Disk ou Gaussian Blue noise dans un premier temps (si le temps le permet, vous pourrez faire les deux), et ensuite regarder Hammersley / Sobol 2D. :::danger Pour la construction des échantillonneurs, vous pouvez partir de la base de code de `whitenoise.cpp` (duplication du fichier + nouvelles entrées dans `CMakeLists.txt`) ::: # Stratified Sampling  4. Implémentez un échantillonneur stratifié pour $n=m^2$ samples. 5. Sur le test d'intégration du disque, observez sa vitesse de convergence asymptotique de l'erreur de l'estimateur Monte-Carlo associé. Vous devez déjà observer une convergence de l'erreur quadratique en $O\left(\frac{1}{n\sqrt{n}}\right)$ à comparer à la convergence de WN en $O\left(\frac{1}{n}\right)$. 6. En dimension supérieure, quels seraient les problèmes ? # UTK The UTK tool kit aims at providing executables to generate and analyze point sets in unit domains $[0,1)^s$. It is originally meant to help researchers developing sampling patterns in a numerical integration using Monte Carlo estimators. More precisely, it was developed with the precise question of optimizing image synthesis via Path tracing algorithms. UTK is a C++ and python library that implements a large variety of samplers and tools to analyze and compare them (discrepancy evaluation, spectral analysis, numerical integration tests…). 7. Récupérez la dernière version de la bibliothèque `git clone https://github.com/utk-team/utk.git` et suivez les instructions de compilation. 8. Expérimentez les outils de génération de points et d'évaluation de qualité (discrépance, spectres de puissance, intégration). Par exemple, comparez la vitesse de convergence de l'erreur d'intégration sur des fonctions gaussiennes, d'un `whitenoise` et un `Stratified` en dimension 4. :::warning :::spoiler Intégration dans UTK Très souvent, il n'y a pas de formules clauses pour les intégrandes que nous considérons en toute dimension. Pour le test d'intégration, il faut d'abord construire une base de donnée de *groundtruths*. Par exemple, sur des gaussiennes aléatoires en dimension 4 et avec une estimation MC numérique sur 1000000 échantillons : * `./metric/Integration/BuildGaussianIntegrandDatabase -d 4 -m 256 -o GaussIntDatabase.dat -n 1000000` Ensuite, l'évaluation d'un pointset * `./metric/Integration/GaussianIntegrationTest -i pointset.dat -f database4d.dat` ::: # Poisson Disk Sampling L'échantillonnage par disques de Poisson (parfois appelé *hardcore point process*) est un grand classique pour le placement d'objets (*decals*) et historiquement l'intégration Monte-Carlo. :::success **Rem.**: Pour ce dernier point, une étude récente[^variance] démontre que les propriétés spectrales des processus Poisson Disk limite l'intérêt de ces approches pour de l'intégration (spécifiquement le comportement asymptotique de la variance de l'estimateur MC est comparable à ceux de WN). ::: Le principe est de garantir qu'aucun échantillon n'est à une distance inférieure à un certain rayon $r$ d'un autre. À l'usage, on préfère paramétrer l'algorithme par un nombre d'échantillons plutôt qu'un nombre de points. Pour un rayon donné $r$, le nombre de points maximal est celui donné par un packing optimal de boules de rayon $r$. En dimension 2 cela correspond à la grille hexagonale. En dimension $s$, un usage classique est de considérer $$ r(n) = \frac{1}{2}\left( \frac{\gamma_s\Gamma(\frac{s}{2}+1)}{n\pi^{s/2}}\right)^{1/s} $$ :::success :::spoiler Démonstration Notons $V_s(r)$ le volume d'une boule de dimension s. On a alors : $V_s(r) = \frac{\pi^{s/2}}{\Gamma(\frac{s}{2} + 1)}r^s$. Alors, $n$ boules de rayon $r$ dans le cube unité occupent une fraction du cube égale à $n V_s(r) / 1^s$. Par ailleurs, l'arrangement *optimal* de sphères dans un carré occupe une proportion $\gamma_s$. Donc, le rayon permettant d'obtenir $n$ sphères packées de manière optimales vérifie : $n V_s(r) = \gamma_s$, soit, après quelques manipulations algébriques : $r^s = \gamma_s / (nV_s(1)) = \gamma_s \frac{\Gamma(\frac{s}{2} + 1)}{n \pi^{s/2}}$. Le packing optimal étant très difficile à trouver par rejet (de probabilité nulle en réalité), il convient de choisir un rayon légèrement plus petit pour être sûr de trouver une solution. Le facteur $1/2$ est arbitraire. ::: La constante $\gamma_s$ est explicite pour des dimensions inférieures à 8 (cf [DT dans utk](https://github.com/utk-team/utk/blob/c64718c91cd05ecd7cec6626eca11d15b6fe736d/include/utk/samplers/SamplerDartThrowing.hpp#L175)). En 2d, $\gamma_s=\frac{\pi\sqrt{3}}{6}$. Pour la fonction $\Gamma(x)$ peut être obtenue via [std::tgamma](https://en.cppreference.com/w/cpp/numeric/math/tgamma).  :::danger Pour une discussion relative à la gestion des bords (toriques ou bornés) et la métrique euclidienne associée, cf section GBN plus bas. ::: ## Approche *Dart throwing* 7. Implémentez l'échantillonneur Poisson Disk naif: pour chaque échantillon candidat (issu d'un WN), on regarde la distance min de ce point à l'ensemble déjà construit, si la distance min est inférieure au rayon $r$, ce candidat est rejeté. 8. Évaluez les performances en temps de l'approche et sa complexité asymptotique. 9. **Version avec relaxation**: si trop d'échecs sont observés, vous pouvez augmenter le rayon avec une loi géométrique ## Approche Bridson Une approximation très efficace a été proposée par [Bridon](https://www.cs.ubc.ca/~rbridson/docs/bridson-siggraph07-poissondisk.pdf)[^1]. Elle consiste à transférer un coût algorithmique sur un coût en mémoire. L'algorithme est le suivant :  En pratique, il vous faut donc: * une grille 2D de taille $r/\sqrt{n}$ contenant 0 ou 1 point * pour valider un point, on ne regarde que les distances aux points dans les cases voisines de $x_i$. 10. implémentez cette version et comparer ses performances (en mémoire et en temps) par rapport à la version *Dart Throwing* :::success **Rem.** Dans la version originale, il est suggéré d'utiliser une grille en dimension $s$ comme "cache" pour accélérer les tests de distance (répondre aux requêtes "$case\rightarrow point$" et "$point\rightarrow case$" -par arrondi-). Dans [UTK](https://utk-team.github.io/utk/), nous utilisons une structure associative `std::map<Case,Point>`. Les accès ne sont plus en $O(1)$ mais on gagne en mémoire en dimension>2. ::: # Gaussian Blue Noise L'objectif est d'implémenter une stratégie d'échantillonnage visant à optimiser la position des échantillons afin de minimiser une énergie donnée (transport optimal, discrépance...). Spécifiquement, on va s'intéresser à une approche à noyau : [Gaussian Blue Noise](https://dl.acm.org/doi/abs/10.1145/3550454.3555519)[^gbn].  Le principe de GBN[^gbn] est de réduire la variance de la convolution de l'échantillonnage par des noyaux gaussiens. Pour un ensemble de points $X$, l'énergie à minimiser est ici : $$ \mathcal{E}(X) = \frac{\pi\sigma^2}{2N}\sum_{k=1}^n\sum_{l=1}^n \exp\left({-\frac{\|x_k - x_l \|^2_2}{2\sigma^2}}\right) $$ Clairement, l'évaluation de cette énergie est quadratique en nombre de points. 10. Dupliquez `whitenoise.cpp` et écrire le code évaluant l'énergie associée à un ensemble de points. Pour minimiser cette énergie, nous allons utiliser une descente sur le gradient $\nabla\mathcal{E}$. Pour un échantillon $x_k$, le gradient de l'énergie est simplement donnée par $$ \nabla\mathcal{E}(x_k) = -\frac{\pi}{N}\sum_{l\neq k}^n \exp\left({-\frac{\|x_k - x_l \|^2_2}{2\sigma^2}}\right)(x_k - x_l) $$ 11. Implémentez l'optimisation d'un ensemble de point $X^0$ (par exemple issu d'un WN), par une simple descente de gradient $x_k^{p+1} = x^{p} - \lambda\nabla\mathcal{E}(x_k)$ pour un learning rate $\lambda$ donné. Le critère d'arret pouvant être un nombre max d'itérations ou une stabilisation de l'énergie (*eg.* la norme du gradient). Le paramètre $\sigma$ du noyau contrôle la diffusion et les interactions entre échantillons. En pratique, un $\sigma=1/\sqrt{N}$ est recommandé par les auteurs (pour un échantillonnage sur un carré unité). :::danger Attention, lorsque les échantillons sont déplacés, ceux-ci peuvent être amenés à sortir du domaine. Dans ce tp, on vous propose de "clamper" les positions dans $[0,1)^2$. Pour s'adapter à des situations de rendu pour lequels une périodisation du domaine est importante, il faut prendre une distance euclidienne **torique**, [cf ici](https://github.com/utk-team/utk/blob/c64718c91cd05ecd7cec6626eca11d15b6fe736d/externals/SinglePeak/common.hh#L124), et faire les translations "modulo 1". ::: 12. Évaluer la qualité de cet échantillonneur en intégration (aire du disque ou UTK) et ses propriétés spectrales. :::success **Rem.** : * Cette approche s'étend de manière triviale en dimensions supérieures. La difficulté porte alors sur le nombre d'itérations pour obtenir un point set de qualité, et la paramétrisation de la taille du noyau $\sigma$. * Dans l'énoncé, nous échantillonnons $[0,1)^2$ pour une métrique euclidienne dans les noyaux gaussiens. Dans GBN[^gbn], les auteurs discutent d'une adaptation de meilleure qualité sur un domaine borné (non torique donc). ::: # Échantillonneurs basse discrépance Nous allons maintenant explorer quelques échantillonneurs basse discrépance. La plupart se basent sur une construction algébrique $\mathbb{N}\rightarrow[0,1)$.  ## Warmup: Van der Corput Un des éléments clefs pour les samplers algébriques réside dans la représentation en base $b$ d'indice et la notion d'inversion de radicale. Pour une représentation $(a_0,a_1,\ldots,a_{m-1})_b$ en base $b$ d'un entier $a$ sur $m$ digits ($a = \sum_{i=0}^{m-1} a_ib^i$), l'inversion de radicale est l'entier $a'$ obtenu par $a'=VdC(a) = (a_{m-1},a_{m-2},\ldots,a_0)_b$. 13. Pour un entier (non signé) sur 32bits en base 2, implémentez cette inversion de radicale (cf versions rapides ci-dessous). Si maintenant vous définissez le 'ieme' échantillon du sampler 1D `uint32_t`$\rightarrow$`[0,1)`: samplerVdC(i):=$\frac{VdC(i)}{2^{32}}$, observez la distribution des premières valeurs que vous obtenez. ```c++= //Code from http://holger.dammertz.org/stuff/notes_HammersleyOnHemisphere.html static uint32_t radicalInverse_VdC(uint32_t bits) { bits = (bits << 16u) | (bits >> 16u); bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u); bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u); bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u); bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u); return bits; } static uint64_t radicalInverse_VdC64(uint64_t bits) { uint64_t n0 = radicalInverse_VdC((uint32_t) bits); uint64_t n1 = radicalInverse_VdC((uint32_t) (bits >> 32)); return (n0 << 32) | n1; } ``` ## Hammersley Hammersley est un des échantillonneurs 2d basse discrépance les plus simples. Pour un $n$ donné, les échantillons sont donnés par $$\left\{\left(\frac{i}{n}, \frac{VdC(i)}{2^{32}}\right), 0\leq i <n\right\}$$ Par construction, cet ensemble de points n'engendre pas une séquence (si je veux $n+1$ points, il faut reconstruire l'ensemble complet). 14. Implémentez cet échantillonneur et validez sa basse discrépance expérimentalement. Vous devez observer une discrépance en $O(log(n)^2/n)$. ## Sampleurs algébriques : Larcher-Pillichshammer L'idée est maintenant de décrire le processus d'échantillonnage par un produit matrice / vecteur en base $b$. On parle alors de matrices génératrices, une par dimension. Spécifiquement, on se place dans un corps de Galois en base $b$, $b$ premier. La j-ième coordonnée dans [0,1) du point d'indice $a=(a_0,a_1,\ldots,a_{m-1})_b$, générée par la matrice $C_j$ de taille $m\times m$ dans GF(b) est donnée par $$ \left(a'_{0},a'_{1},\ldots,a'_{m-1}\right) = C_j\cdot \left(\begin{array}{c}a_0\\a_1\\\ldots\\ a_{m-1}\end{array}\right)\\ x^{(j)}_a = \sum_i^m a'_i b^{-i-1} $$ :::danger Attention, les opérations arithmétiques sont à faire en GF(b). Dans ce cas particulier où seulement des sommes et des produits sont effectués, les calculs peuvent être faits dans $\mathbb{Z}$ avec un `modublo b` à la fin. En base 2, on utilisera plutôt les opérations sur les représentations des entiers (AND, XOR). ::: 15. Implémentez la construction d'un échantillon par produit matrice / vecteur (taille m). En 2d, vous pouvez utiliser les matices suivantes: $$ \begin{align} C_0&= \left(\begin{array}{ccc}0....01\\ 0....1 0\\ 0 10..0\\ 10.....\end{array}\right) \quad \text{(anti-diagonale)}\\ C_1 &= \left(\begin{array}{ccc}1 1 1..1\\ 0 1 1..1\\ 0..0 11\\ 0....01\end{array}\right) \quad \text{(matrice triangulaire supp à 1)} \end{align} $$ :::success **Rem.** Cette paire de matrices engendre un ensemble basse discrépance de Larcher–Pillichshammer[^LP] parmi les plus efficaces en discrépance 2D. ::: 16. Évaluez les performances en discrépance de ce générateur. ## Sampleurs algébriques : Sobol L'échantillonneur de [Sobol](https://en.wikipedia.org/wiki/Sobol_sequence) suit cette approche algébrique permettant de construire des matrices $C_j$ avec des propriétés intéressantes. En vrac : * l'expansion des matrices $(m\times m)\rightarrow (m+1 \times m+1)$ suit une construction purement analytique (construction par récurrence sur des [polynômes primitifs](https://en.wikipedia.org/wiki/Primitive_polynomial_(field_theory))); * n'importe quel sous-ensemble produit une $(t,s)-$sequence; * des accélérations significatives par codes de Gray permettent des implémentations très efficaces. Sobol se construit sur deux choses : une séquence de polynômes primitifs de degré croissant et un vecteur générateur (*direction number*, un par polynôme). Supposons un polynôme $p(x)=a_ex^e + a_{e-1}x^{e-1} + ... + a_0$ à coefficients dans $GF(b)$. Démarrons la construction de la matrice $C_{p(x)}$ par un bloc $e\times e$ à valeurs dans $GF(b)$ qui soit *non-singular upper triangular (NUT)*. Ensuite, les colonnes sont complétées par récurrence. La colonne $V_n$ ($e<n\leq m$) est donnée par $$ V_{n} = \tilde{V}_{n-e} - \sum_{i=1}^{e} a_{e-i} V_{n-i} $$ où $\tilde{V}_{n-e}$ est la colonne ${V}_{n-e}$ de $C_{p(x)}$ décalée vers le bas et complétée de zéro. :::warning Exemple au tableau ::: En pratique, la liste des polynômes primitifs est connue [Sloane base 2](https://oeis.org/A058947) ou [Sloane base 3](https://oeis.org/A058944). Concernant les blocs $e\times e$, c'est un levier pour l'optimisation. On peut s'intéresser à la meilleure initialisation pour une certaines qualité [Joe&Kuo](https://web.maths.unsw.edu.au/~fkuo/sobol/) ont fait ce travail et beaucoup d'implémentations de Sobol' utilisent ces tables. Quelle que soit l'initialisation, une collection de $s$ matrices de Sobol aura la propriété de $(t,m,s)-$séquence avec un $t = \sum_{d=0}^{s-1} (e_d -1)$. 17. Dans [Sobol-UTK](https://github.com/utk-team/utk/blob/master/data/Sobol/new-joe-kuo-6.21201) ou Joe & Kuo, regardez le format de représentation des générateurs de Sobol. 18. En base 2, regardez l'implémentation dans UTK de [l'échantillonneur de Sobol](https://github.com/utk-team/utk/blob/master/include/utk/samplers/SamplerSobol.hpp) avec à la fois la construction de la matrice ($m_k$ dans le code), et la génération des points. En utilisant l'outil en ligne de commande, évaluez les propriétés des points de Sobol générés par la table Joe&Kuo. :::warning :::spoiler * `d`: dimension * `s`: degré * `a`: les coefs (sans $x^s$ et sans "+1") * `m`: partie $e\times e$ ::: :::success **Rem.** Pour aller plus loin sur la génération de matrices ad hoc, cf [matbuilder](https://projet.liris.cnrs.fr/matbuilder/). ::: ## Scrambling Par construction, ces échantillonneurs basse discrépance sont parfaitement déterministes. Dans certaines situations, par exemple pour décorréler les échantillons utilisés pour des intégrations Monte Carlo dans des pixels "espace écran" (par exemple pour du [screen space blue noise](https://dl.acm.org/doi/abs/10.1145/3306307.3328191)[^ssbn]), il peut être intéressant de randomiser un ensemble de points existant. | CP | Digital Shift | Owen| | -------- | -------- | 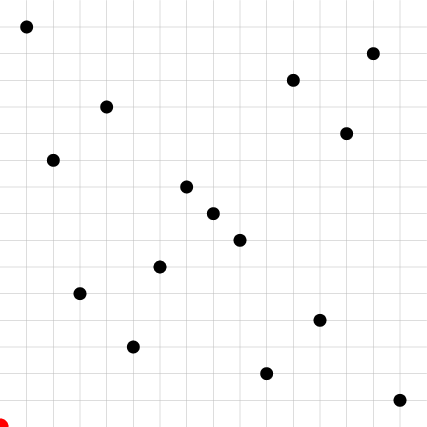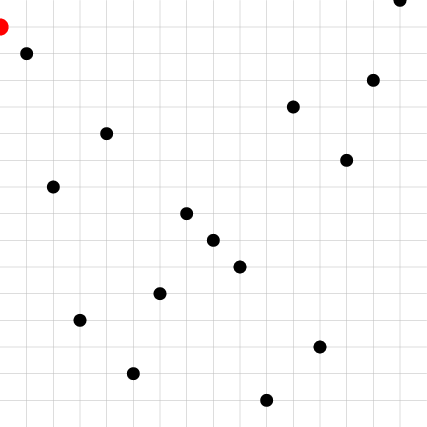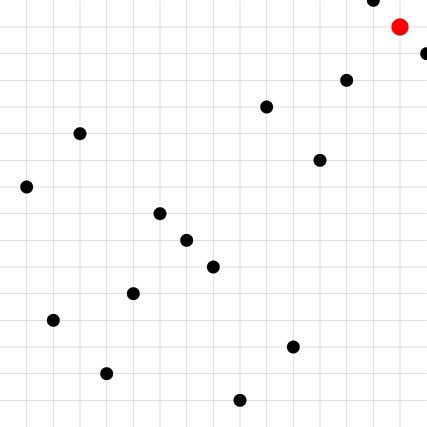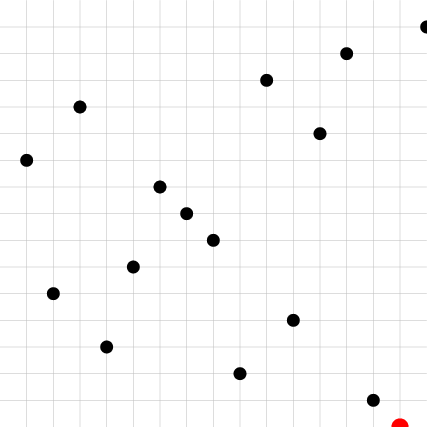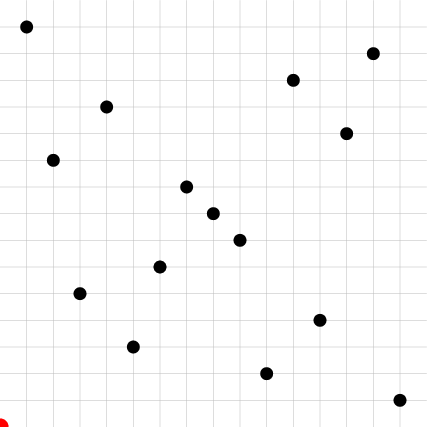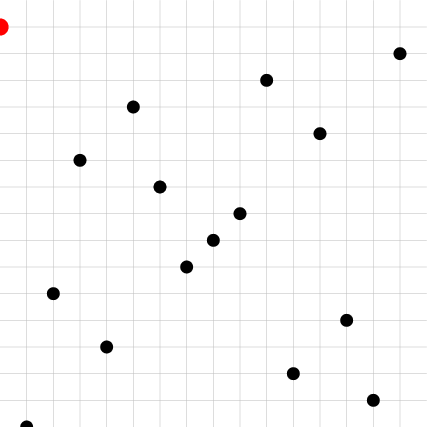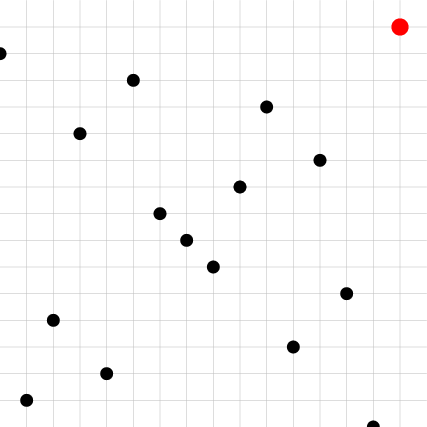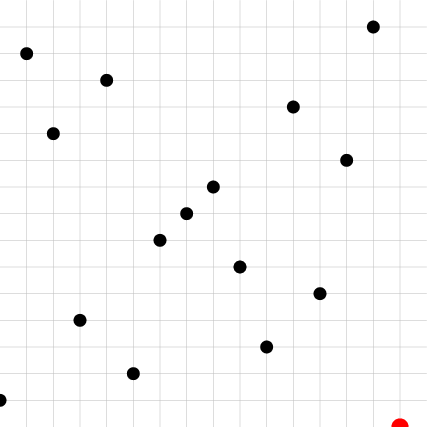-------- | |  |  |  | * **Rotation de Cranley-Patterson**: fixons $r\approx\mathcal{U}(0,1)$, les points sont translatés de manière torique d'un vecteur $r$: $$ x = x + r \quad mod \,1 $$ * **Digital Random Shift**: cette approche est définie sur la représentation entière en base 2 des échantillons. Pour un entier "r" aléatoire (par ex sur 32 bits), la sommation est remplacée par un XOR (a est ici la représentation entière --32bits par ex-- d'un point dans [0,1), *eg.* $a= x^{(j)}_a\cdot2^{32}$): $$ a = a \, XOR\, r $$ * **Owen Scrambling[^owen]**: tout comme le digital shift, le scrambling d'Owen préserve les propriétés de $(t,m,s)$-net des samplers LDS. Ce scrambling se caractérise par un arbre $\Sigma$ de profondeur $m$ où chaque flag booléen, noté $\sigma_{(..)}$, à chaque noeud, est *XORé* avec les digits de $a$ : $$ \begin{align*} &b_0 = \sigma_{(\cdot)}\oplus a_0\\ &b_1 = \sigma_{(a_0)}\oplus a_1\\ &b_2 = \sigma_{(a_0,a_1)}\oplus a_2\\ &\ldots\\ &b_{n-1} = \sigma_{(a_0,a_1,\ldots, a_{n-2})}\oplus a_{n-1}\,.\\ \end{align*} $$ Cet échantillonneur casse le caractère "séquence" des échantillonneurs (il faut aller jusqu'aux feuilles pour connaitre la position des points), est plus coûteux en mémoire, mais offre une randomisation permettant de casser significativement des structures qui pourraient apparaitre dans les échantillons de Sobol. Par ailleurs, dans des contextes d'intégration de fonctions lisses, le scrambling d'Owen permet un gain significatif en convergence[^owensmooth]. De nombreuses implémentations efficaces existent [ici](https://andrew-helmer.github.io/tree-shuffling/) et [ici](https://jcgt.org/published/0009/04/01/). | Input | Owen -x- | Owen -y- | 2D | | -------- | -------- | -------- | -- | |  |  |  | | 17. Implémentez un scrambling par Digital Shift et vérifiez la préservation de la discrépance. 18. En utilisant les outils de UTK, vérifiez que le scrambling d'Owen préserve également la discrépance. # Et en dimension supérieure ? Pour les échantillonneurs de type Poisson disks ou ceux basés sur un modèle énergétique (transport optimal, méthodes à noyaux), la construction de points *blue noise* en grande dimension est souvent problématique. Par exemple, l'approche [SOT](https://perso.liris.cnrs.fr/david.coeurjolly/publication/paulin-2020/) vise à approximer l'énergie de transport en haute dimension par une approche *sliced* pour en pratique pouvoir obtenir des échantillons de qualité. Naturellement, les samplers basse-discrépance vont très souvent avoir des extensions en dimension supérieures par construction. C'est le cas pour [Sobol](https://en.wikipedia.org/wiki/Sobol_sequence), mais aussi [Halton](https://en.wikipedia.org/wiki/Halton_sequence) ou [Faure](http://mint.sbg.ac.at/desc_SFaure-ori.html). Ainsi, en dimension $s$, la propriété de $(t,m,s)-$net est atteignable sans un coût algorithmique trop important. 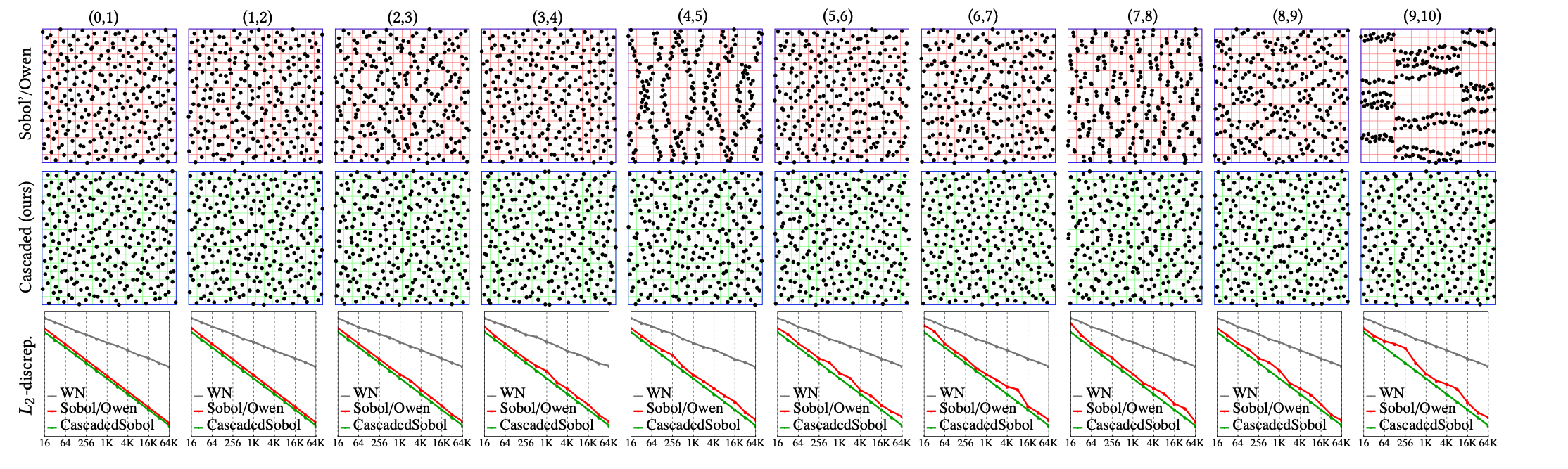Cependant, si on regarde certaines projections 2D d'un sampler LDS (Sobol) de dimension 11 (première ligne):  On peut observer de gros défaut d'uniformité qui pourrait être critique en intégration si l'intégrande est fortement séparable sur ces projections. Il y a un intérêt à travailler spécifiquement sur certaines projections de l'espace d'intégration ([matbuilder](https://projet.liris.cnrs.fr/matbuilder/) ou [Cascaded Sobol'](https://perso.liris.cnrs.fr/david.coeurjolly/publication/cascaded-2021/) -seconde ligne de l'image ci-dessus-). Une autre stratégie très utilisée dans des moteurs de rendu consiste à opérer un *pairing*: supposons que nous avons deux ensembles 2D de bonne qualité (quelle que soit la métrique), peut-on construire un ensemble 4d préservant certaines propriétés ? Expérimentons les différentes stratégies. 19. Prenez deux ensembles 2D (par exemple des réalisations de Larcher-Pillichshammer ou Sobol-01). Construisez un sampler 4d par un *pairing* aléatoire des échantillons. En utilisant les outils de UTK, évaluez les qualités de cet échantillonneur 4d en discrépance et intégration (par rapport par exemple à un WN ou un Sobol 4d d'UTK). 20. Reprenez le même principe en utilisant une séquence de Sobol des indices pour le *pairing*. Évaluez également ces points 4d. # References [^1]: Bridson, Robert. "Fast Poisson disk sampling in arbitrary dimensions." SIGGRAPH sketches 10.1 (2007): 1. [^variance]: Pilleboue, A., Singh, G., Coeurjolly, D., Kazhdan, M., & Ostromoukhov, V. (2015). Variance analysis for Monte Carlo integration. ACM Transactions on Graphics (TOG), 34(4), 1-14. [^gbn]: Ahmed, A. G., Ren, J., & Wonka, P. (2022). Gaussian blue noise. ACM Transactions on Graphics (TOG), 41(6), 1-15. [^LP]: G Larcher and F Pillichshammer. 2003. Sums of Distances to the Nearest Integer and the Discrepancy of Digital Nets. Acta Arithmetica 106 (2003), 379–408. [^ssbn]: Heitz, Eric, Laurent Belcour, Victor Ostromoukhov, David Coeurjolly, and Jean-Claude Iehl. "A low-discrepancy sampler that distributes Monte Carlo errors as a blue noise in screen space." In ACM SIGGRAPH 2019 Talks, pp. 1-2. 2019). [^owen]: Owen, A. B. (1998). Scrambling Sobol'and Niederreiter–Xing Points. Journal of complexity, 14(4), 466-489. [^owensmooth]: Owen, Art B. "Scrambled net variance for integrals of smooth functions." The Annals of Statistics 25, no. 4 (1997): 1541-1562.