Markov chains: exercises === [TOC] ### Exercise 1: Calculation of transition probabilities Three black and three white balls are distributed in two urns in sucha a way that each contains three balls. We say that the system is in state $i$, $i = 0,1,2$ or $3$ if the first urn contain $i$ white balls. At each step, we draw one ball from each urn and place the ball drawn for the first urn into the second and conversely with one ball from the second urn. Let $X_t$ denote the state of the system after the $t$^th step. Explain why $(X_t)_{t\ge 0}$ is a Markov chain and calculate its transition probability matrix. ### Exercise 2: Time homogeneous Markov chain Consider the process $(X_t)_{t\ge 0}$ which takes the values $0, 1$ or $2$. Suppose $$P(X_{t+1} = j | X_t = i, X_{t-1} = i_{t_1},...,X_0 = i_0) = \begin{cases} R_{ij} & \text{when $t$ is even} \\ Q_{ij} & \text{when $t$ is odd} \end{cases}$$ where $R$ and $Q$ are 3x3 matrices such as, for all $i = 0, 1$ or $2$, $R_{i0}+R_{i1}+R_{i2} = Q_{i0}+Q_{i1}+Q_{i2} = 1$. Is $(X_t)_{t\ge0}$ a time-homogeneous Markov chain? If not, then show how, by enlarging the state space, we may transform it into a time-homogeneous Markov chain. ### Exercise 3: Nucleotide substitution model Let us consider the markov chain describing the state of a DNA nucleotide at each generation. $E = \{A, C, T, G\}$. The probability of transversion (purine <-> pyrimidine) is given by $\alpha$ and the probability of transition (purine <-> purine or pyrimidine <-> pyrimidine) is given by $\beta$. The probability that no mutation occurs is given by $\gamma$ as illustrated on this figure:  1. Determine the value of $\gamma$. 2. Write the transition matrix. 3. Determine the stationary distribution if they exist. 4. Complete the following table (assuming in all cases $\alpha + \beta < 1$). Then in each cases, determine if the distribution converges to the stationary distribution (starting from an arbitrary state). | $\alpha$ | $\beta$ | Chain irreducible? | Chain aperiodic? | | -------- | ------- | ------------------ | ---------------- | | $=0$ | $>0$ | yes/no | yes/no | | $>0$ | $=0$ | yes/no | yes/no | | $>0$ | $>0$ | yes/no | yes/no | ### Exercise 4: Classification of states, the frog. A frog jumps between 7 lily pads according to this figure.  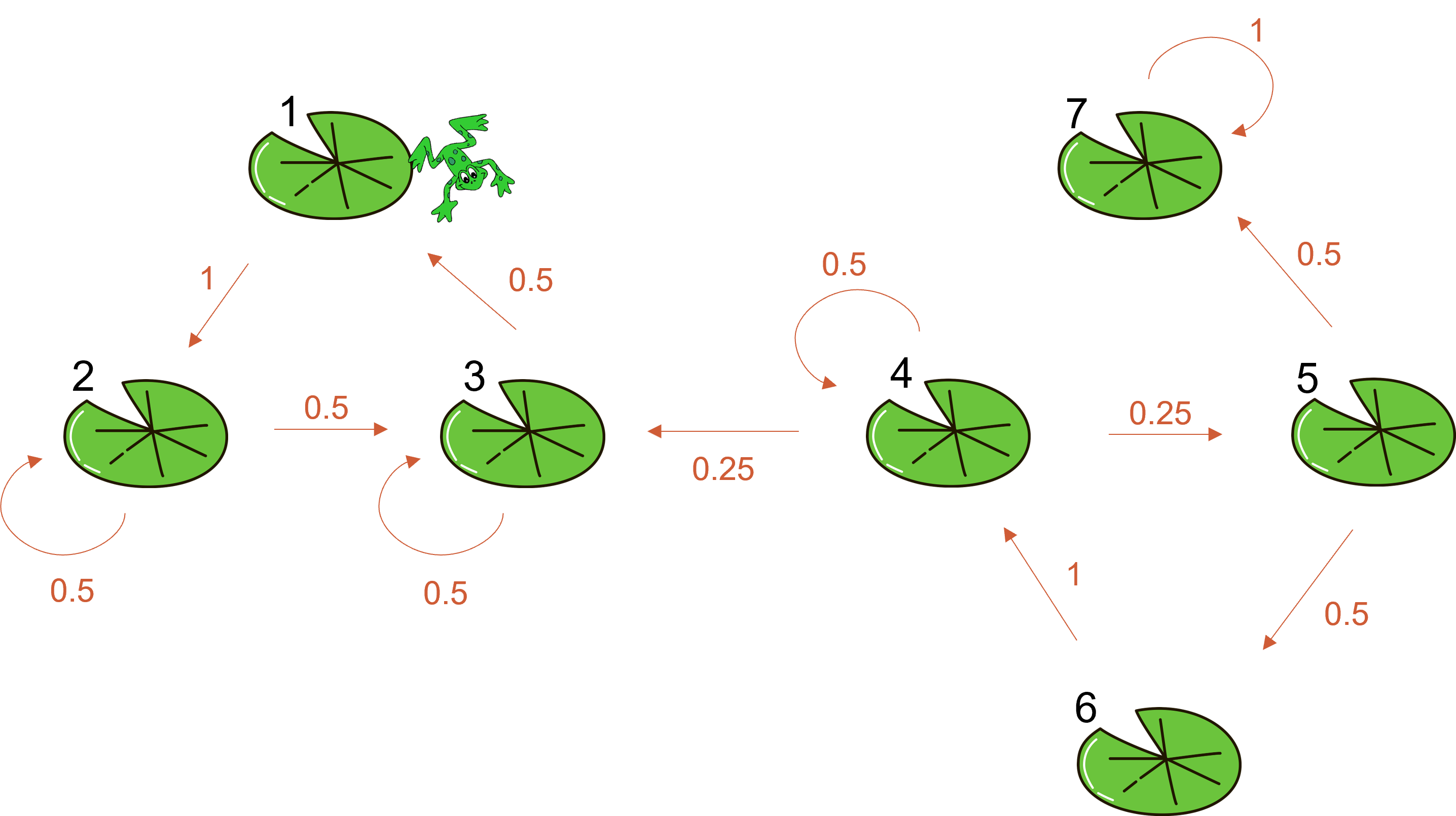1. Determine the transition matrix. 2. Determine the partition of the state space in communicating classes. Which classes are recurrent and which one are transient? 3. Starting in tate 1, what is the probability that we are still in state 1 after 3 steps? After 5 steps? After 1000 steps? 4. Starting in state 4, what is the probability that we ever reach state 7? 5. Starting in state 4, how long on average does it take to reach either 3 or 7?