# Segmentation d'image - modèles hybrides ## (Traitement et Analyse d'Image 5d) > > [name=Jacques-Olivier Lachaud][time=Decembre 2020][color=#907bf7] Laboratoire de Mathématiques, Université Savoie Mont Blanc > (Les images peuvent être soumises à des droits d'auteur. Elles sont utilisées ici exclusivement dans un but pédagogique) ###### tags: `info911` Retour à [INFO911 (Main) Traitement et analyse d'image](https://codimd.math.cnrs.fr/s/UE_B59gMy) --- # Modèles hybrides pour la segmentation :::danger Objectifs d'une **bonne** segmentation mal définie approches régions et contours peuvent donner des résultats intéressants, mais: * stabilité du résultat en fonction d'une variation de l'entrée ou des paramètres ? * comment faire cohabiter information de région et information de contour ? * sortie = résultat d'un algorithme, mais pas d'un modèle attendu ::: :::info Nécessité de construire des **modèles** définissant l'attendu, avant de mettre au point des algorithmes pour trouver la meilleure solution (modèle variationnel). ::: > Apparition de modèles dans les années 1990 [color=#907bf7] --- ## Principaux modèles :::success * Modèle de Mumford-Shah [1989] * Snakes / contours actifs / contours actifs géodésiques [1989 -- 1998] * Modèle de Chan-Vese [2001] * Modèle Variation Totale [Rudin, Osher, Fatemi 1992 ] ::: :::success * Approches bayesiennes par champ de markov [1984] * Approches graphes et optimisation par graph-cut [2000] ::: :::info Pour chaque résultat $u$, chaque modèle définit une **énergie** $E(u)$ Un algorithme d'**optimisation** cherche ensuite le $u_{opt}$ qui minimise $E(u)$ ::: --- # Modèles "continus" :::success * Modèle de Mumford-Shah [1989] * Snakes / contours actifs / contours actifs géodésiques [1989 -- 1998] * Modèle de Chan-Vese [2001] * Modèle Variation Totale [Rudin, Osher, Fatemi 1992 ] ::: --- ## Le modèle de Mumford-Shah [1989] **Input**: fonction image $g$ de domaine $\Omega$. **Energie**: soit $K$ un ensemble de contours et une fonction $u$ lisse sur $\Omega \setminus K$. $$ E(u,K)=\alpha \underbrace{\int_\Omega |g-u|^2}_\text{attache aux données} + \beta \underbrace{\int_{\Omega \setminus K} |\nabla u |^2}_\text{reconstruction lisse} + \gamma \underbrace{\mathrm{Longueur}(K)}_\text{géométrie simple} $$ :::warning Problème: trouver $u_{opt},K_{opt}$ qui minimise $E$ ::: ==Intuitivement== régions homogènes sinon 1er et 2e termes coûteux, $K$ placé sur les contours sinon 2e terme coûteux, pas trop de contours sinon 3e terme coûteux --- ## Modèle de Mumford Shah: exemples de résultats [2017] | Image $g$ | reconstruction $u$, contour $K$ en rouge | |:---------------------------------------------------------------------------------------------------------:|:----------------------------------------------------------------------------------------------------------:| |  |  | --- ## Modèle de Mumford Shah: exemples de résultats [2017] | Input $g$ | MS $\alpha=1, \beta=1, \gamma=0.01$ | MS $\alpha=0.01, \beta=1, \gamma=0.001$ | | -------- | -------- | -------- | |  | |  | `at-grad`, `segmentation-mumford-shah-color` --- ## Intérêts/défauts du modèle de Mumford-Shah :::success * formulation unifiant **homogénéité** des régions et **hétérogénéité** des contours * contrainte **géométrique** sur les régions (périmètre court) * inspiration de centaines de méthodes et de milliers d'articles ::: :::danger * énergie non convexe => pas d'algorithme simple d'optimisation * dans cette formulation, aucun algorithme praticable d'optimisation * grand espace des paramètres * coût en calcul important (ici 1min) ::: --- ## Snakes, contours actifs [Kass, Witkin, Terzopoulos 1992] Soit $C(t)=(x(t),y(t))$ une courbe paramètrique, $t \in [0,1]$ $$ E(C)=\int_0^1 \underbrace{-\|\nabla I(x(t),y(t))\|^2}_\text{attache aux contours} +\alpha \underbrace{(x'(t)^2+y'(t)^2)}_{\approx\text{longueur}}+\beta \underbrace{(x''(t)^2+y''(t)^2)}_{\approx\text{courbure}} dt $$ On cherche $C_{opt}=\arg\min_C E(C)$ :::success Recherche les forts gradients, donc les contours. Favorise des courbes lisses. Plus facile à coder (en 2D), rapide, interactif. ::: :::danger Optimisation très sensible à l'initialisation. Cherche une forme simple. 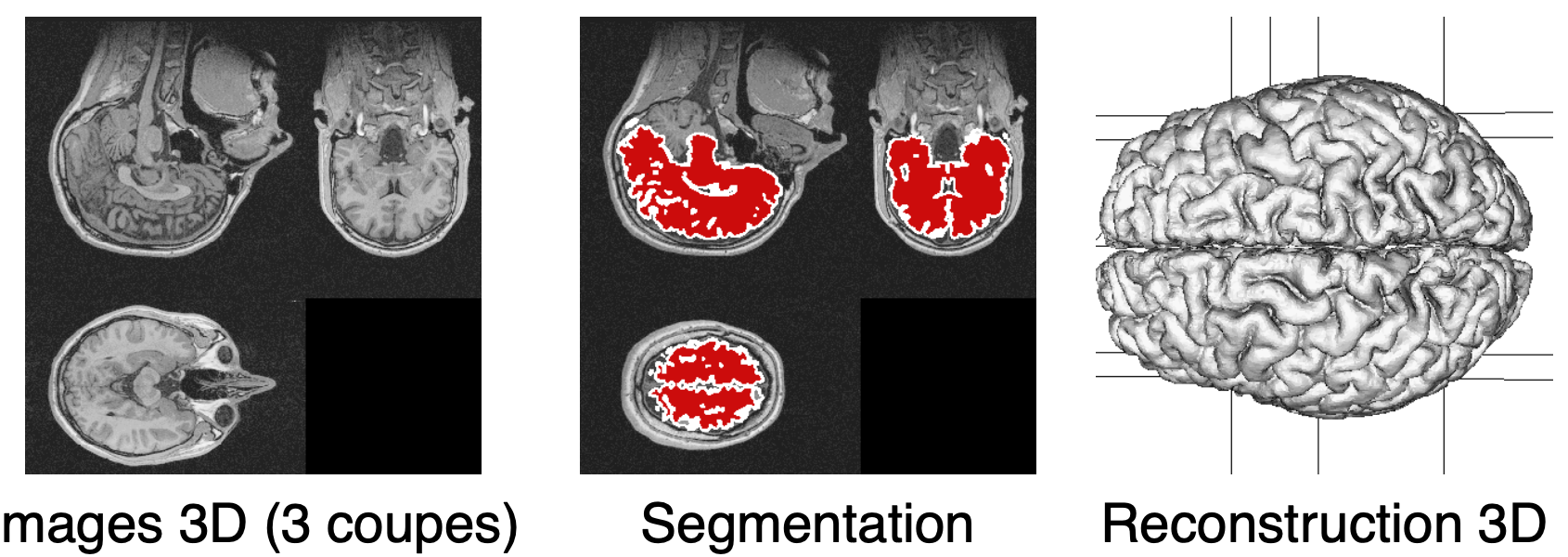::: --- ## Snakes : exemple de résultats 2D  --- ## Snakes : exemple de résultats 3D [2004] Surface triangulée déformable  --- ## Modèle de Chan-Vese [2001] Modèle efficace pour segmentation en objet / fond ## Modèle Variation Totale [Rudin, Osher, Fatemi 1992 ] Modèle surtout efficace en restauration d'image, et inpainting. --- # Modèles "discrets" :::success * Approches bayesiennes par champ de markov [1984] * Approches graphes et optimisation par graph-cut [2000] ::: --- ## Approches graphes et optimisation par graph-cut [2000] Domaine transformé en graphe $G:=(V \cup \{s,t\},E)$ où $V$=pixels, plus deux noeuds $s,t$  Poids $w(s,p)$ : attache à la région 1, e.g. $w(s,p):=|I(p)-\textrm{moyenne}(R_1)|$ Poids $w(t,p)$ : attache à la région 2, e.g. $w(s,p):=|I(p)-\textrm{moyenne}(R_2)|$ Poids $w(p,q)$ : coût du contour, e.g. $\lambda$ ==Coupe== dans $G$: $C \subset E$ tel que $s$ et $t$ séparés par $C$ ==Coupe minimal==: on cherche $C_{opt}$ qui minimise $\sum_{e \in C} w(e)$ --- ## grabcut: exemple de résultats En bleu, pixels associés au fond $s$, en rouge pixels associés à l'objet | | | | -------- | -------- | |  |  | Attache aux données: Gaussian Mixture Model et champ de Markov `grabcut` `video-grabcut` --- ## Some comparisons